方べきの定理

方べきの定理　　　関連問題

【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。

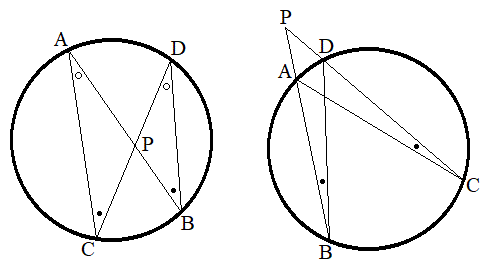方べきの定理(1)：円の2弦AB，CDの交点(交点が円内)、もしくは、2弦BA，CDの延長線の交点(交点が円外)をPとすると、

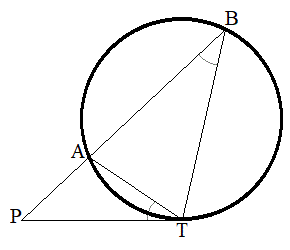方べきの定理(2)：円外の点Pから円に接線PTを引き、Pから円と2点A，Bで交わるように直線を引くとき、

方べきの定理(1)の証明：交点Pが円内の場合、△PAC，△PDBにおいて、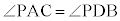

(円周角)，

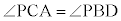(円周角)より、

△PAC ∽ △PDB

よって、PA：PD = PC：PB　∴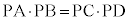

交点Pが円外の場合、△PAC，△PDBにおいて、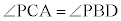

(円周角)，

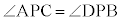(共通)より、

△PAC ∽ △PDB

よって、PA：PD = PC：PB　∴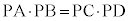

方べきの定理(2)の証明：△PTAと△PBTにおいて、接弦角の定理より、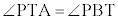

，

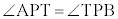(共通)より、

△PTA ∽ △PBT

よって、PA：PT = PT：PB　∴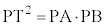

【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。

【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。

【広告】広告はここまでです。

苦学楽学塾 随時入会受付中！
理系大学受験ネット塾苦学楽学塾
(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。