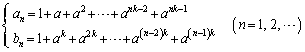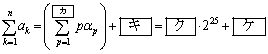数列演習問題2008年(私大編)
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
[1](等差数列) 初項が80,公差が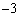 の等差数列の初項から第n項までの和が最大となるのは、n= のときで、その和は である。
の等差数列の初項から第n項までの和が最大となるのは、n= のときで、その和は である。
(日大文理'08)
[解答へ]
[2](等差数列) 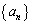 が初項9,公差2の等差数列であるとき、
が初項9,公差2の等差数列であるとき、
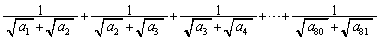 =
=
(東京薬科大'08)
[解答へ]
[3](等差数列) 数列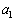 ,
,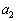 ,・・・,
,・・・,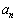 ,・・・は、初項a,公差dの等差数列であり、
,・・・は、初項a,公差dの等差数列であり、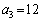 かつ
かつ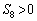 ,
,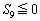 をみたす。ただし、
をみたす。ただし、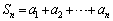 である。このとき、次の各問に答えよ。
である。このとき、次の各問に答えよ。
(1) 公差dがとる値の範囲を求めよ。
(2) 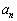 (
(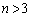 )がとる値の範囲をnを用いて表せ。
)がとる値の範囲をnを用いて表せ。 (3) 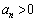 ,
,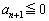 となるnの値を求めよ。
となるnの値を求めよ。 (4) 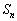 が最大となるときのnの値をすべて求めよ。また、そのときの
が最大となるときのnの値をすべて求めよ。また、そのときの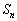 をdの式で表せ。
をdの式で表せ。 (早大政経'08)
[解答へ]
[4](等差数列、等比数列、対数) 関数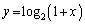 の表す曲線上に点
の表す曲線上に点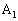 ,
,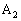 ,・・・,
,・・・,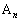 ,・・・がある。
,・・・がある。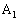 の座標は
の座標は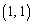 で、
で、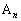 の座標を
の座標を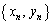 (
(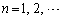 )とおくとき、数列
)とおくとき、数列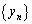 は等差数列で公差が
は等差数列で公差が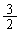 である。以下の設問で、必要ならば
である。以下の設問で、必要ならば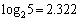 を用いよ。
を用いよ。
(1) 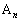 の座標は である。
の座標は である。 (2) 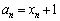 (
(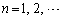 )とおくと、数列
)とおくと、数列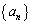 は初項 ,公比 の等比数列となる。また、不等式
は初項 ,公比 の等比数列となる。また、不等式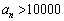 を満たす最小の自然数nは である。
を満たす最小の自然数nは である。 (北里大薬'08)
[解答へ]
[5](等差数列、等比数列、整数) 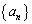 を初項
を初項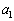 が7で公差が3の等差数列とし、
が7で公差が3の等差数列とし、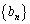 を初項
を初項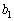 が1で公差が5の等差数列とする。Aを数列
が1で公差が5の等差数列とする。Aを数列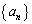 の項として現れるすべての数の集合、Bを数列
の項として現れるすべての数の集合、Bを数列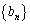 の項として現れるすべての数の集合とし、
の項として現れるすべての数の集合とし、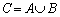 とする。
とする。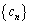 をCの要素を重複を許さずに小さい順にならべて得られる数列として、以下の問いに答えよ。
をCの要素を重複を許さずに小さい順にならべて得られる数列として、以下の問いに答えよ。
(1) 数列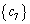 の第7項
の第7項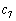 は で、第11項
は で、第11項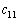 は である。
は である。
(2) 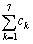 = で、
= で、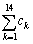 = である。
= である。
一般に、mを正の整数としたとき、
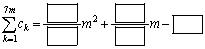
である。
(3) 数列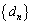 を、
を、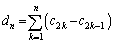 と定める。このとき、数列
と定める。このとき、数列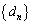 の第77項
の第77項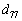 は で、第80項
は で、第80項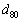 は である。
は である。
(慶大商'08)
[解答へ]
[6](等比数列) 数列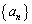 が
が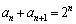 (
(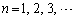 )をみたすとき、
)をみたすとき、
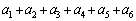 =
=
さらに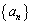 が等比数列であるとき、
が等比数列であるとき、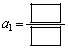 ,
,
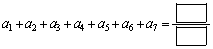 である。
である。
(大同工大'08)
[解答へ]
[7](等比数列) a,kを2以上の自然数とするとき、数列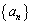 ,
,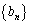 を
を
で定義する。このとき、次の問に答えよ。
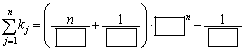
(1) 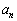 ,
,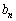 の値を求めよ。
の値を求めよ。 (2) 任意の自然数nに対して、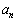 は
は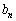 で割り切れることを示せ。
で割り切れることを示せ。 (3) 等式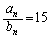 が任意の自然数nに対して成立するような組(a,k)をすべて求めよ。
が任意の自然数nに対して成立するような組(a,k)をすべて求めよ。 (武蔵工大電気電子・建築'08)
[解答へ]
[8](等比数列) nを2以上の自然数とする。集合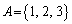 と集合
と集合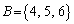 から次の2つの規則で有限数列
から次の2つの規則で有限数列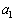 ,
,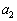 ,・・・,
,・・・,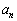 をつくる。
をつくる。
規則1: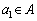 である。
である。 規則2: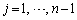 に対し、
に対し、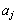 が偶数ならば
が偶数ならば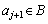 であり、
であり、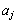 が奇数ならば
が奇数ならば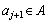 である。
である。 (1) 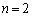 のとき、数列
のとき、数列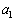 ,
,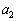 は全部で 通りある。その中で
は全部で 通りある。その中で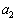 が奇数になる数列
が奇数になる数列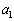 ,
,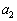 は全部で 通りある。
は全部で 通りある。 (2) 一般のnに対し、数列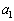 ,・・・,
,・・・,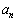 は全部で
は全部で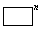 通りある。その中で
通りある。その中で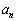 が奇数になる数列は全部で
が奇数になる数列は全部で 通りある。
(3) nを固定し、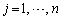 とする。数列
とする。数列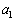 ,・・・,
,・・・,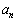 の中で
の中で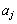 が奇数になる数列は全部で
が奇数になる数列は全部で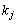 通りであるとする。このとき、
通りであるとする。このとき、 である。
(上智大理工A'08)
[解答へ]
[9](数列の和) 次の数列の和を求めよ。
(1) 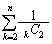 (神戸薬大'08)
(神戸薬大'08)
(2) 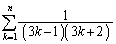 (昭和薬大'08)
(昭和薬大'08)
(3) 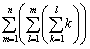 (中部大'08改)
(中部大'08改)
(4) 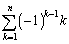 (摂南大'08改)
(摂南大'08改)
(5) 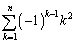 (関西学院大経済'08改)
(関西学院大経済'08改)
[解答へ]
[10](数列の和) 正の整数nに対して、「偶数ならば2で割り、奇数ならば1を引いて2で割る」という操作を値が1になるまで繰り返し行うときの操作回数を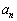 とする。ただし、
とする。ただし、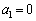 とする。たとえば、
とする。たとえば、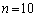 のとき、値は10→5→2→1のように3回の操作で1になるから、
のとき、値は10→5→2→1のように3回の操作で1になるから、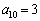 である。
である。
(1) 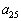 = ア である。また、
= ア である。また、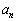 = ア が成り立つのは、 イ ≦n≦ ウ のときである。
= ア が成り立つのは、 イ ≦n≦ ウ のときである。 (2) pを正の整数とする。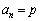 を満たす最小のnは エ である。また、
を満たす最小のnは エ である。また、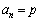 を満たすnの個数を
を満たすnの個数を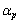 とすると、
とすると、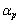 = オ である。
= オ である。 (3) 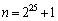 とすると、
とすると、 である。
(法政大理工'08)
[解答へ]
[11](群数列) 数列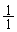 ,
,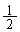 ,
,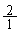 ,
,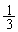 ,
,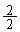 ,
,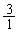 ,
,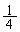 ,
,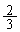 ,
,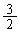 ,
,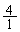 ,
,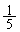 ,・・・ において、
,・・・ において、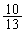 が最初に現れる項は第 であり、また、第2450項は
が最初に現れる項は第 であり、また、第2450項は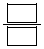 である。
である。
(星薬大'08)
[解答へ]
[12](格子点、階差数列) 座標平面上の点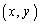 において、x,yがともに整数となる点を格子点という。いま、格子点
において、x,yがともに整数となる点を格子点という。いま、格子点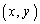 のx座標とy座標の和
のx座標とy座標の和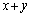 を、この格子点の値と定義する。
を、この格子点の値と定義する。
連立方程式
で表される領域内にある格子点について、それぞれ格子点の値を定め、その総和を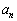 とする。
とする。
(2) 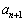 を
を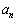 とnを用いて表せ。
とnを用いて表せ。 (3) 数列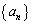 の一般項を求めよ。
の一般項を求めよ。 (立命館大'08)
[解答へ]
[13](漸化式) 正の整数nに対して、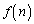 と
と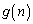 は0以上の整数で、次の条件(i),(ii),(iii)をみたしている。
は0以上の整数で、次の条件(i),(ii),(iii)をみたしている。
(i) 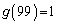 ,
,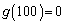
(ii) 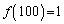
(iii) 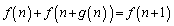
このとき、次の設問に答えよ。
(1) 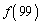 を求めよ。
を求めよ。 (2) 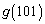 を求めよ。
を求めよ。 (3) 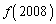 を求めよ。
を求めよ。 (早大商'08)
[解答へ]
[14](二項定理) 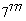 の下3桁を求めよ。
の下3桁を求めよ。
(東京理科大理'08改)
[解答へ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。