四分位数 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
ある一つの属性についてのデータ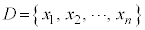 の要素を
の要素を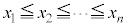 となるように並べ、ほぼ同数の4つに分けるとき、分け目の境界に来る数を四分位数と言う。四分位数を小さい方から第1四分位数、第2四分位数、第3四分位数と言う。
となるように並べ、ほぼ同数の4つに分けるとき、分け目の境界に来る数を四分位数と言う。四分位数を小さい方から第1四分位数、第2四分位数、第3四分位数と言う。
現行教科書では、データの大きさを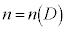 として、四分位数を以下の手順で求めている。
として、四分位数を以下の手順で求めている。
・nが奇数のとき、中央値 を第2四分位数
を第2四分位数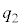 とする。データDから中央値
とする。データDから中央値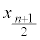 を除いて、データDを前半
を除いて、データDを前半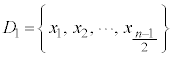 と後半
と後半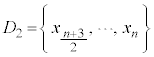 に分け、
に分け、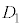 の中央値を第1四分位数
の中央値を第1四分位数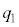 、
、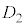 の中央値を第3四分位数
の中央値を第3四分位数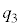 とする。
とする。 ・nが偶数のとき、中央値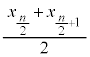 を第2四分位数
を第2四分位数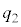 とする。データDを前半
とする。データDを前半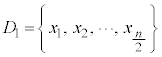 と後半
と後半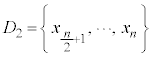 に分け、
に分け、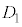 の中央値を第1四分位数
の中央値を第1四分位数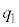 、
、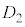 の中央値を第3四分位数
の中央値を第3四分位数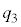 とする。
とする。 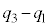 を四分位範囲、
を四分位範囲、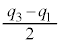 を四分位偏差と言う。
を四分位偏差と言う。
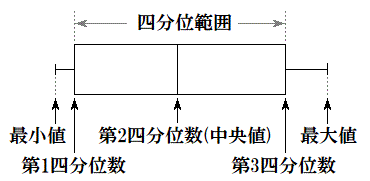 右図のように、
右図のように、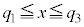 の範囲を箱で示し、
の範囲を箱で示し、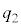 の位置に線分を引き、さらに、最大値、最小値と箱を線分で結んだ図を箱ひげ図と言う。
の位置に線分を引き、さらに、最大値、最小値と箱を線分で結んだ図を箱ひげ図と言う。
高校教科書の四分位数は、表計算ソフトEXCELのQUARTILE関数(データの25%,50%,75%相当の位置にある数値)と定義が違うので注意してください。データの大きさが奇数の場合には、QUARTILE.EXC関数の結果とは一致します。
 奇数個7個のデータ
奇数個7個のデータ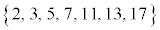 の場合、中央値の7が第2四分位数です。7を除いた前半
の場合、中央値の7が第2四分位数です。7を除いた前半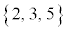 の中央値3が第1四分位数です。後半
の中央値3が第1四分位数です。後半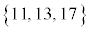 の中央値13が第3四分位数です。四分位範囲は
の中央値13が第3四分位数です。四分位範囲は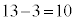 ,四分位偏差は
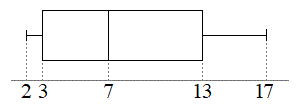
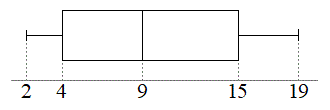
,四分位偏差は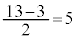 です。箱ひげ図は右図のようになります。
です。箱ひげ図は右図のようになります。
 偶数個8個のデータ
偶数個8個のデータ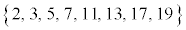 の場合、中央値
の場合、中央値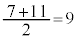 が第2四分位数です。前半
が第2四分位数です。前半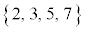 の中央値
の中央値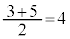 が第1四分位数、後半
が第1四分位数、後半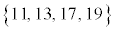 の中央値
の中央値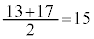 が第3四分位数です。四分位範囲は
が第3四分位数です。四分位範囲は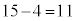 ,四分位偏差は
,四分位偏差は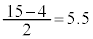 です。
です。
データの整理で取り上げたデータを再掲します。
| 日 | 最高気温 | 日照時間 | 湿度 | 日 | 最高気温 | 日照時間 | 湿度 | 日 | 最高気温 | 日照時間 | 湿度 |
| 1 | 21.4 | 0 | 71 | 11 | 27.6 | 2.7 | 54 | 21 | 29.3 | 11.4 | 31 |
| 2 | 25.2 | 0.9 | 67 | 12 | 23.5 | 0.9 | 71 | 22 | 31.9 | 6.0 | 46 |
| 3 | 24.7 | 1.4 | 67 | 13 | 26.7 | 7.9 | 37 | 23 | 30.0 | 8.1 | 34 |
| 4 | 24.0 | 0.3 | 71 | 14 | 25.2 | 1.0 | 58 | 24 | 26.2 | 7.9 | 50 |
| 5 | 26.9 | 6.4 | 57 | 15 | 26.3 | 8.6 | 51 | 25 | 27.3 | 8.2 | 46 |
| 6 | 24.9 | 6.5 | 53 | 16 | 27.2 | 5.4 | 45 | 26 | 19.8 | 0.7 | 70 |
| 7 | 26.3 | 9.6 | 44 | 17 | 25.3 | 1.8 | 56 | 27 | 24.9 | 10.5 | 48 |
| 8 | 19.7 | 0 | 68 | 18 | 25.3 | 0 | 71 | 28 | 25.9 | 7.0 | 47 |
| 9 | 28.4 | 6.8 | 55 | 19 | 27.6 | 11.4 | 46 | 29 | 27.7 | 5.7 | 48 |
| 10 | 29.7 | 8.2 | 42 | 20 | 29.0 | 7.8 | 38 | 30 | 27.8 | 7.9 | 48 |
最高気温の30個のデータを小さい順に並べると、
19.7, 19.8, 21.4, 23.5, 24, 24.7, 24.9, 24.9, 25.2, 25.2, 25.3, 25.3, 25.9, 26.2, 26.3, 26.3, 26.7, 26.9, 27.2, 27.3, 27.6, 27.6, 27.7, 27.8, 28.4, 29, 29.3, 29.7, 30, 31.9
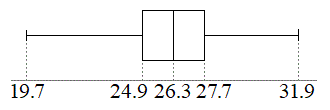 となります。15番目と16番目がともに26.3で中央値、即ち第2四分位数は26.3℃です。データを1番目から15番目までと16番目から30番目までに分けると、前半の8番目は24.9で、前半の中央値、即ち第1四分位数は24.9℃です。後半の8番目は27.7で、後半の中央値、即ち第3四分位数は27.7℃です。箱ひげ図は右図のようになります。ばらつきが小さく中央値付近に集中している状況が分かります。
となります。15番目と16番目がともに26.3で中央値、即ち第2四分位数は26.3℃です。データを1番目から15番目までと16番目から30番目までに分けると、前半の8番目は24.9で、前半の中央値、即ち第1四分位数は24.9℃です。後半の8番目は27.7で、後半の中央値、即ち第3四分位数は27.7℃です。箱ひげ図は右図のようになります。ばらつきが小さく中央値付近に集中している状況が分かります。
日照時間の30個のデータを小さい順に並べると、
0, 0, 0, 0.3, 0.7, 0.9, 0.9, 1, 1.4, 1.8, 2.7, 5.4, 5.7, 6, 6.4, 6.5, 6.8, 7, 7.8, 7.9, 7.9, 7.9, 8.1, 8.2, 8.2, 8.6, 9.6, 10.5, 11.4, 11.4
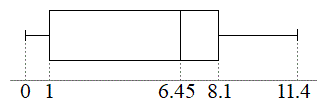 となります。15番目が6.4,16番目が6.5で中央値、即ち第2四分位数は6.45時間です。データを1番目から15番目までと16番目から30番目までに分けると、前半の8番目は1で、前半の中央値、即ち第1四分位数は1時間です。後半の8番目は8.1で、後半の中央値、即ち第3四分位数は8.1時間です。箱ひげ図は右図のようになります。ばらつきの大きい状況が分かります。
となります。15番目が6.4,16番目が6.5で中央値、即ち第2四分位数は6.45時間です。データを1番目から15番目までと16番目から30番目までに分けると、前半の8番目は1で、前半の中央値、即ち第1四分位数は1時間です。後半の8番目は8.1で、後半の中央値、即ち第3四分位数は8.1時間です。箱ひげ図は右図のようになります。ばらつきの大きい状況が分かります。
湿度の30個のデータを小さい順に並べると、
31, 34, 37, 38, 42, 44, 45, 46, 46, 46, 47, 48, 48, 48, 50, 51, 53, 54, 55, 56, 57, 58, 67, 67, 68, 70, 71, 71, 71, 71
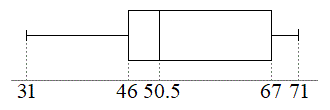 となります。15番目が50,16番目が51で中央値、即ち第2四分位数は50.5%です。データを1番目から15番目までと16番目から30番目までに分けると、前半の8番目は46で、前半の中央値、即ち第1四分位数は46%です。後半の8番目は67で、後半の中央値、即ち第3四分位数は67%です。箱ひげ図は右図のようになります。
となります。15番目が50,16番目が51で中央値、即ち第2四分位数は50.5%です。データを1番目から15番目までと16番目から30番目までに分けると、前半の8番目は46で、前半の中央値、即ち第1四分位数は46%です。後半の8番目は67で、後半の中央値、即ち第3四分位数は67%です。箱ひげ図は右図のようになります。
9月を記した上記データと同じ都市の最高気温について、各月ごとの四分位数を1年間まとめると以下の表のようになります。
| 月 | 最小値 | 第1四分位数 | 第2四分位数 | 第3四分位数 | 最大値 |
| 1月 | -2.0 | 1.3 | 3.9 | 6.4 | 11.3 |
| 2月 | 0.1 | 4.0 | 7.25 | 11.9 | 19.1 |
| 3月 | 3.7 | 11.7 | 13.8 | 18.5 | 23.9 |
| 4月 | 10.5 | 15.0 | 18.05 | 21.8 | 24.2 |
| 5月 | 16.5 | 20.7 | 22.9 | 24.9 | 28.9 |
| 6月 | 21.5 | 25.8 | 27.4 | 28.8 | 32.1 |
| 7月 | 23.2 | 27.6 | 30.8 | 33.4 | 35.4 |
| 8月 | 21.7 | 28.0 | 31.9 | 33.5 | 37.3 |
| 9月 | 19.7 | 24.9 | 26.3 | 27.7 | 31.9 |
| 10月 | 11.9 | 15.9 | 19.6 | 27.3 | 29.0 |
| 11月 | 5.1 | 13.8 | 15.65 | 16.6 | 19.3 |
| 12月 | -2.6 | 4.2 | 6.7 | 9.7 | 14.1 |
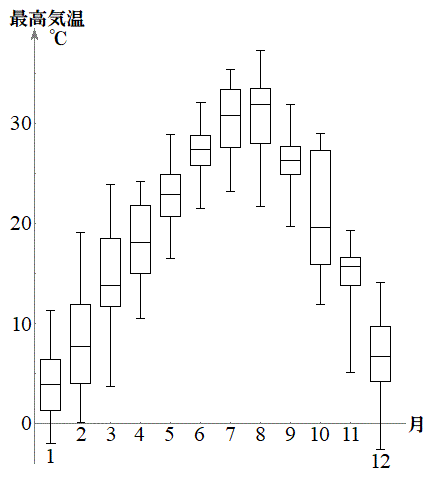 この表に基づいて、最高気温の各月の箱ひげ図を1年間まとめてグラフに表すと、右図のようになります。1年間の気温の変化の具合をよく伝えています。
この表に基づいて、最高気温の各月の箱ひげ図を1年間まとめてグラフに表すと、右図のようになります。1年間の気温の変化の具合をよく伝えています。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 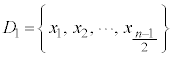 と後半
と後半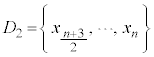 に分け、
に分け、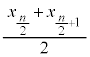 を第2四分位数
を第2四分位数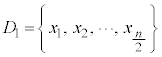 と後半
と後半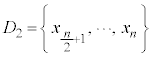 に分け、
に分け、