代表値 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
ある一つの属性についてのデータ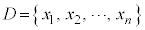 があるとき、集合Dの要素の個数
があるとき、集合Dの要素の個数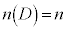 をデータの大きさと言う。データの総和をデータの大きさで割ったもの、
をデータの大きさと言う。データの総和をデータの大きさで割ったもの、
をデータの平均値と言う。
度数が最も多い階級の階級値を最頻値(mode)と言う。
データを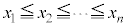 となるように並べたときに中央に来る値、つまり、nが奇数のときは、
となるように並べたときに中央に来る値、つまり、nが奇数のときは、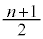 番目の値
番目の値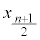 、nが偶数のときは、
、nが偶数のときは、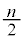 番目に来る値と
番目に来る値と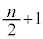 番目に来る値の平均
番目に来る値の平均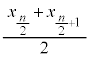 を中央値(median)と言う。
を中央値(median)と言う。
データの整理で取り上げたデータを再掲します。
| 日 | 最高気温 | 日照時間 | 湿度 | 日 | 最高気温 | 日照時間 | 湿度 | 日 | 最高気温 | 日照時間 | 湿度 |
| 1 | 21.4 | 0 | 71 | 11 | 27.6 | 2.7 | 54 | 21 | 29.3 | 11.4 | 31 |
| 2 | 25.2 | 0.9 | 67 | 12 | 23.5 | 0.9 | 71 | 22 | 31.9 | 6.0 | 46 |
| 3 | 24.7 | 1.4 | 67 | 13 | 26.7 | 7.9 | 37 | 23 | 30.0 | 8.1 | 34 |
| 4 | 24.0 | 0.3 | 71 | 14 | 25.2 | 1.0 | 58 | 24 | 26.2 | 7.9 | 50 |
| 5 | 26.9 | 6.4 | 57 | 15 | 26.3 | 8.6 | 51 | 25 | 27.3 | 8.2 | 46 |
| 6 | 24.9 | 6.5 | 53 | 16 | 27.2 | 5.4 | 45 | 26 | 19.8 | 0.7 | 70 |
| 7 | 26.3 | 9.6 | 44 | 17 | 25.3 | 1.8 | 56 | 27 | 24.9 | 10.5 | 48 |
| 8 | 19.7 | 0 | 68 | 18 | 25.3 | 0 | 71 | 28 | 25.9 | 7.0 | 47 |
| 9 | 28.4 | 6.8 | 55 | 19 | 27.6 | 11.4 | 46 | 29 | 27.7 | 5.7 | 48 |
| 10 | 29.7 | 8.2 | 42 | 20 | 29.0 | 7.8 | 38 | 30 | 27.8 | 7.9 | 48 |
30日分の最高気温のデータを、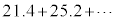 という具合に足していくと、総和は、785.7になります。最高気温の平均値は、
という具合に足していくと、総和は、785.7になります。最高気温の平均値は、
より、26.19℃です。このとき電卓でもあれば、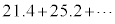 と足していってもよいのですが、暗算では大変です。そこで、仮平均との差の平均を考える、という技巧があります。最高気温の最大値は22日の31.9℃、最小値は8日の19.7℃なので、
と足していってもよいのですが、暗算では大変です。そこで、仮平均との差の平均を考える、という技巧があります。最高気温の最大値は22日の31.9℃、最小値は8日の19.7℃なので、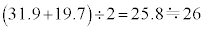 なので、仮平均を26℃として、各データの26℃との差を
なので、仮平均を26℃として、各データの26℃との差を
というように足していきます。これなら、暗算でもできないことはありません。平均値は、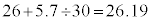 として求めることができます。入試でも功を奏する技巧です。但し、仮平均の技巧は、日照時間や湿度のようにばらつきが多いデータだとあまり効果はありません。日照時間の平均値は、
として求めることができます。入試でも功を奏する技巧です。但し、仮平均の技巧は、日照時間や湿度のようにばらつきが多いデータだとあまり効果はありません。日照時間の平均値は、
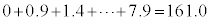 ,
,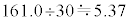
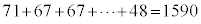 ,
,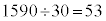
最高気温の最頻値は、データの整理で書いたような幅1.5℃の階級では、24.5以上26未満の階級の度数8が最大の度数なので、最頻値は、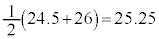 ℃です。
℃です。
日照時間の最頻値は、度数9が最大の0以上1.5未満の階級なので、0.75時間です。日照時間の平均時間5.37時間とは大きくずれます。
湿度の最頻値は、度数10が最大の40以上50未満の階級なので、45%です。
最高気温の中央値は、最高気温を小さい順に並べたとき、15番目の26.3℃と16番目の平均26.3℃の平均をとり、26.3℃です(上記のデータでは中央に来るものが存在しませんが、データの大きさが奇数なら、ちょうど中央に来るものが存在します)。
日照時間の中央値は、日照時間を小さい順に並べたとき、15番目の6.4と16番目の6.5の平均をとり、6.45時間です。
湿度の中央値は、湿度を小さい順に並べたとき、15番目の50と16番目の51の平均をとり50.5%です。
平均値、最頻値、中央値のどれがデータの代表値として適当か、ということについては、データの特性にもよります。例えば、日本人100人の平均年収が400万円と言われても、年収1億円の人が2人いて、残りの98人の年収が200万円であっても平均年収396万円ということになりますが、これは年収の実体を反映しているとは言えません。最頻値や中央値の方が実体を表しているということもあります。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 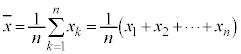
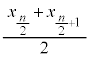 を中央値(median)と言う。
を中央値(median)と言う。