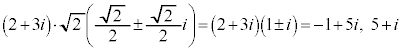複素数の回転 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
複素数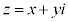 (x,yは実数、iは虚数単位)を極形式で表し、
(x,yは実数、iは虚数単位)を極形式で表し、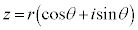 ,但し、
,但し、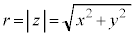 ,
,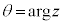
ここで、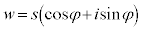 ,
,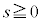 として、zにwをかけるとき、
として、zにwをかけるとき、
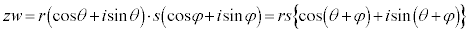
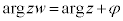 ,
,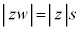 より、複素数平面上でzは、大きさがs倍され、原点(極)の回りに反時計回りにφだけ回転した位置に来ます、
より、複素数平面上でzは、大きさがs倍され、原点(極)の回りに反時計回りにφだけ回転した位置に来ます、
[例1] 平面上の点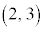 を、原点の回りに反時計回りに
を、原点の回りに反時計回りに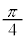 ,
,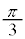 ,
,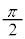 ,
,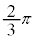 回転すると、点
回転すると、点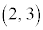 を表す複素数は
を表す複素数は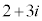 なので、
なので、
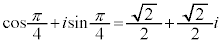
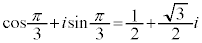
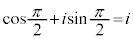
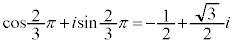
より、それぞれ、
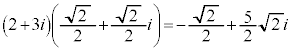
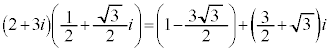
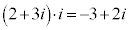
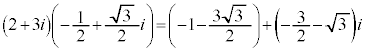
よって、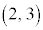 は、それぞれ、
は、それぞれ、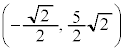 ,
,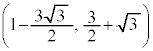 ,
,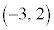 ,
,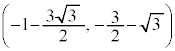 に来ます。
に来ます。
[例2] 原点Oと平面上の点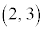 を結ぶ線分を1辺とする正三角形のもう一つの頂点を求めます。
を結ぶ線分を1辺とする正三角形のもう一つの頂点を求めます。
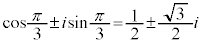
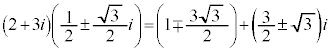 (複合同順)
(複合同順)
よって、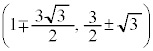 (複合同順)
(複合同順)
[例3] 原点Oと平面上の点A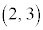 に対して
に対して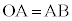 ,
,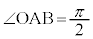 となる直角二等辺三角形のもう一つの頂点Bを求めます。
となる直角二等辺三角形のもう一つの頂点Bを求めます。
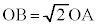 ,
,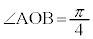 より、原点の回りに
より、原点の回りに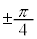 回転して、大きさを
回転して、大きさを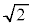 倍するために、
倍するために、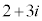 に
に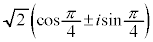 をかけます。
をかけます。
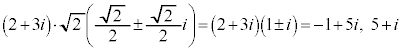
よって、Bは、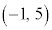 または
または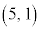 です。
です。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 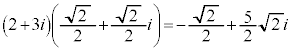
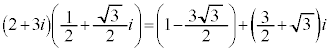
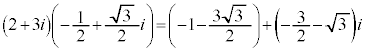
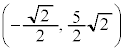 ,
,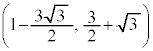 ,
,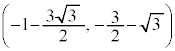 に来ます。
に来ます。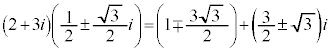 (複合同順)
(複合同順)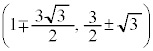 (複合同順)
(複合同順)