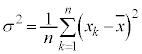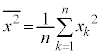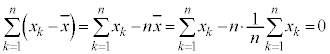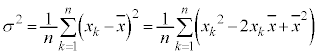���U�ƕW�����@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�����̑����ɂ��Ẵf�[�^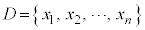 �̕��ϒl��
�̕��ϒl��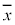 �Ƃ���Ƃ��AD�̊e�v�f�ƕ��ϒl�Ƃ̍������ƌ����B����2��̕��ϒl�A
�Ƃ���Ƃ��AD�̊e�v�f�ƕ��ϒl�Ƃ̍������ƌ����B����2��̕��ϒl�A
�����U�ƌ����B�܂��A���U�̕�����σ���W�����ƌ����B�f�[�^�̗v�f��2��̕��ϒl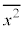 ��
��
�Ƃ���ƁA���U�́A
�Ƃ��Čv�Z�ł���B�܂�A2��̕��ς��畽�ς�2��������ƕ��U�ɂȂ�B
���̍��ڂɂ��ẮA�u���ۂ�������1��E2020�N�Łv(�����o��)�̌c���w��w��[3]�̉̉�����ɏ������L�����Q�Ƃ��Ă��������B
���v�f�[�^�̂���ɂ��ĕ��͂��悤�Ƃ���Ƃ��A�f�[�^�̊e�v�f�̕��̑��a���l����ƁA
�ƂȂ��Ă��܂��̂ŁA�a��0�ɂȂ�Ȃ��悤�ɕ���2��̘a�̕��ϒl���l�������̂����U�ł��B���U�ł�2��̘a�Ȃ̂ŁA���U�̕������ł���W���������߁A�W�����ɂ���ăf�[�^�̂���ׂ܂��B
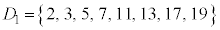 �̕��ϒl�́A
�̕��ϒl�́A
�ł��B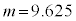 �Ƃ��āA���U
�Ƃ��āA���U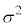 �́A
�́A
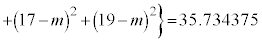 �@����@
�@����@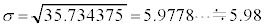 �ł��B
�ł��B
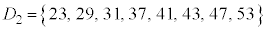 �̕��ϒl��38�C���U��87�C�W������9.33�ŁA
�̕��ϒl��38�C���U��87�C�W������9.33�ŁA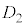 �̕����W����5.98��
�̕����W����5.98��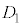 ����������傫���ƌ����܂��B
����������傫���ƌ����܂��B
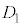 �̗v�f��2��̕��ϒl�́A
�̗v�f��2��̕��ϒl�́A
�����F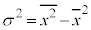 ��p���ĕ��U���v�Z����ƁA
��p���ĕ��U���v�Z����ƁA
�ƂȂ�A�@�ƈ�v���܂��B
�����F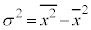 ���m���߂Ă����܂��B
���m���߂Ă����܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B