���H�吔�w'08�N���[1]
���̖₢�ɓ�����B
���݂����Ă���Ƃ���B���̂Ƃ�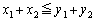 �ł��邱�Ƃ��ؖ�����B
�ł��邱�Ƃ��ؖ�����B (2) n��2�ȏ�̐����Ƃ��A �̎���
�̎���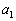 �C
�C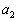 �C����C
�C����C �C
�C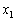 �C
�C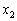 �C����C
�C����C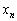 �C
�C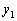 �C
�C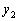 �C����C
�C����C ��
�� �����n�̕s����
 (
(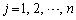 )
)���݂����Ă���Ȃ�A
�ł��邱�Ƃ��ؖ�����B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@
(1)  �@����@
�@����@  �@����A
�@����A
 �@����B
�@����B�@���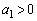 �Ȃ̂ŁA�A���A
�Ȃ̂ŁA�A���A
�@���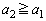 �Ȃ̂ŁA
�Ȃ̂ŁA
���ӂ� ��������ƁA�B���A
��������ƁA�B���A
(2) ���w�I�A�[�@���낤�Ƃ������Ƃ͂��������@�������܂����A�Ȃ��Ȃ��A�[�@�̘g�g�݂������܂���B�����ŁA �̏ꍇ���l���āA
�̏ꍇ���l���āA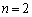 ����
����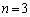 �ւ̘_���̐i��ׂĂ݂܂��B
�ւ̘_���̐i��ׂĂ݂܂��B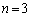 �̂Ƃ��ɂ́A
�̂Ƃ��ɂ́A 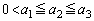 �@����@
�@����@
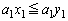 �@����A
�@����A
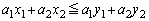 �@����B
�@����B
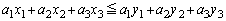 �@����C
�@����C��4������A �����ƂɂȂ�܂��B
�����ƂɂȂ�܂��B
�A�[�@�ɂ��邱�Ƃ��l���āA �̂Ƃ��̌��ʁF
�̂Ƃ��̌��ʁF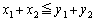 �𗘗p���邱�ƂɂȂ�܂����A�@�C�A�C�B�́A
�𗘗p���邱�ƂɂȂ�܂����A�@�C�A�C�B�́A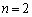 �̂Ƃ��̉���Ɠ����Ȃ̂ŁA���R�A
�̂Ƃ��̉���Ɠ����Ȃ̂ŁA���R�A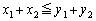 �͐��藧���܂��B(1)�Ɠ��l�ɂ���̂ł���A
�͐��藧���܂��B(1)�Ɠ��l�ɂ���̂ł���A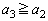 �𗘗p���āA
�𗘗p���āA 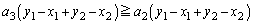 �@����D
�@����D�����ŁA(1)�Ɠ��l�ɇA�ɂ���� �������Ă���̂ŁA
�������Ă���̂ŁA
�������āA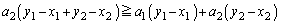
�D�ƂȂ��Ċe�ӂ�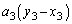 ��������A
��������A 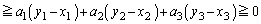 �@(�� �C)
�@(�� �C)�� 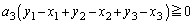
 ���A
���A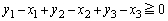
��  �ƂȂ�܂��B
�ƂȂ�܂��B
��ʂ�n�̏ꍇ�ɐ��w�I�A�[�@�̘g�g�݂ɏ悹�邽�߂ɂ́A �̂Ƃ��ɁA
�̂Ƃ��ɁA �Ƃ��邽�߂ɁA �̂Ƃ��́A
�̂Ƃ��́A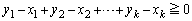 �𗘗p����悢�킯�ł��B�������炳��ɁA
�𗘗p����悢�킯�ł��B�������炳��ɁA �Ƃ��邽�߂ɂ́A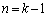 �̂Ƃ��́A
�̂Ƃ��́A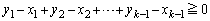 �𗘗p���܂��B
�𗘗p���܂��B
�ȉ��A �C����C
�C����C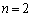 �̂Ƃ��̌��ʂ��g���̂ŁA���w�I�A�[�@�̉���́A�u
�̂Ƃ��̌��ʂ��g���̂ŁA���w�I�A�[�@�̉���́A�u �̂Ƃ���������Ɖ��肷��v�Ƃ����`�ɂȂ�܂��B
�̂Ƃ���������Ɖ��肷��v�Ƃ����`�ɂȂ�܂��B
�������āA���Ă��ȉ��̂悤�ɂ܂Ƃ߂邱�Ƃ��ł���ł��傤�B���w�I�A�[�@�ɂ��ؖ�����B (�T) 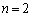 �̂Ƃ��́A(1)�ɂ�萬�藧�B
�̂Ƃ��́A(1)�ɂ�萬�藧�B (�U) 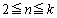 �̂Ƃ��ɐ��藧�Ɖ��肷��B�����A
�̂Ƃ��ɐ��藧�Ɖ��肷��B�����A  �̎���
�̎��� �C
�C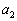 �C����C
�C����C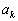 �C
�C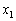 �C
�C �C����C
�C����C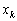 �C
�C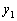 �C
�C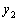 �C����C
�C����C ��
��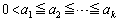 �@����@
�@����@�����k�̕s����
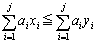 (
(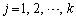 )�@����A
)�@����A���݂����Ă���Ȃ�A
 �@(
�@(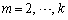 )�@����B
)�@����B����������(�B�̊e�s�����͇A�������Ă͂��߂Đ������܂�)�Ɖ��肷��B
�����ŁA�A�� �̏ꍇ�̕s�����Ƈ@���A
�̏ꍇ�̕s�����Ƈ@���A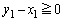 �@����C
�@����C
�܂��A�@�C�A�ɉ����āA3�̎���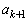 �C
�C �C
�C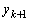 ��
�� ���݂����Ƃ���B
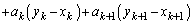 �@(�� �@�C����сA�B��
�@(�� �@�C����сA�B��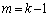 �̏ꍇ)
�̏ꍇ)������
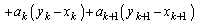 �@(�� �@�C����сA�B��
�@(�� �@�C����сA�B��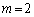 �̏ꍇ)
�̏ꍇ)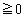 �@(�� �D)
�@(�� �D)�� 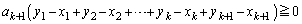
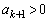 ���A
���A
����āA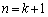 �̂Ƃ��ɂ���������B
�̂Ƃ��ɂ���������B (�T)�C(�U)���A2�ȏ�̐���n�ɂ��Đ�������B�@(�ؖ��I)
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B