���H�吔�w'10�N�O��[2]
a�𐳂̐����Ƃ���B���̎���x�ɂ��Ă̕�����
(��)�@�@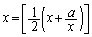
�����������Ȃ��悤��a�����������ɕ��ׂ����̂�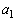 �C
�C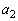 �C
�C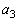 �C��� �Ƃ���B������
�C��� �Ƃ���B������ �̓K�E�X�L���ŁA����u�ɑ��A
�̓K�E�X�L���ŁA����u�ɑ��A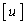 ��u�ȉ��̍ő�̐�����\���B
��u�ȉ��̍ő�̐�����\���B
(1) 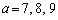 �̊e�X�ɂ���(��)�̉������邩�ǂ����肵�A����ꍇ�͉�x�����߂�B
�̊e�X�ɂ���(��)�̉������邩�ǂ����肵�A����ꍇ�͉�x�����߂�B (2) 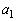 �C
�C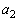 �����߂�B
�����߂�B (3) 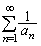 �����߂�B
�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@[1]�Ɠ��l�Ɍ����ڂ͎苭�����ł����A�U���ʂ�ɉ���Η��Ƃ��Ȃ���肾�Ƃ������Ƃ��킩��܂��B
(3)�ł́A�o��҂́A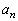 �̌`��f�肷��ۂ̘_�q�����悤�Ƃ��Ă���Ǝv���܂��B
�̌`��f�肷��ۂ̘_�q�����悤�Ƃ��Ă���Ǝv���܂��B
�K�E�X�L���̊�{�́Ax�������Cm�𐮐��Ƃ��āA
�ł��B�{�������ʼn������܂��B��蕶�ł́u���̎���x�v�Ə�����Ă��܂����Ax�ƃK�E�X�L���u���Ă���̂ŁAx�͐��̐����ł��B
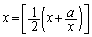 ��
�� 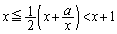
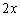 �������āA
�������āA
�e�ӂ���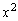 �������A
�������A
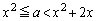 �@����@
�@����@
(1) �@�ɂ����āA
(i) 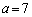 �Ƃ���ƁA
�Ƃ���ƁA �����̕s�����������̐���x�́A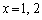 �݂̂ł��B���̂���
�݂̂ł��B���̂���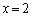 �������E���̕s���������܂��B����āA(��)�̉������݂��A����
�������E���̕s���������܂��B����āA(��)�̉������݂��A����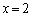 ......[��]
......[��] (ii) 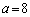 �Ƃ���ƁA
�Ƃ���ƁA �����̕s�����������̐���x�́A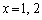 �݂̂ŁA�����Ƃ��E���̕s���������܂���B����āA(��)�̉��͑��݂��܂���B ......[��]
�݂̂ŁA�����Ƃ��E���̕s���������܂���B����āA(��)�̉��͑��݂��܂���B ......[��] (iii) 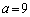 �Ƃ���ƁA
�Ƃ���ƁA �����̕s�����������̐���x�́A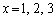 �݂̂ŁA���̂���
�݂̂ŁA���̂���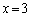 �������E���̕s���������܂��B����āA(��)�̉������݂��A����
�������E���̕s���������܂��B����āA(��)�̉������݂��A����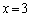 ......[��]
......[��]
(2) 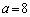 �̂Ƃ�(��)�����������Ȃ��Ƃ���(1)�̌��ʂ��瑦
�̂Ƃ�(��)�����������Ȃ��Ƃ���(1)�̌��ʂ��瑦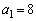 �Ƃ��Ă��܂��̂͑��v�ł��B(1)�ł́A
�Ƃ��Ă��܂��̂͑��v�ł��B(1)�ł́A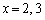 �����ɂȂ��Ă���ꍇ�ׂĂ��܂����Ax�́u���̐����v�Ȃ̂ŁA
�����ɂȂ��Ă���ꍇ�ׂĂ��܂����Ax�́u���̐����v�Ȃ̂ŁA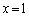 �����ɂȂ�ꍇ�����邩���m��܂���B
�����ɂȂ�ꍇ�����邩���m��܂���B 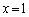 �����ɂȂ�Ƃ��A�@��
�����ɂȂ�Ƃ��A�@��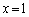 �Ƃ��āAa�́A
�Ƃ��āAa�́A������A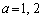 �̂Ƃ��ɁA
�̂Ƃ��ɁA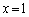 ��(��)�̉��ɂȂ�܂��B
��(��)�̉��ɂȂ�܂��B
���l�ɁA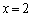 �����ɂȂ�Ƃ��A�@��
�����ɂȂ�Ƃ��A�@��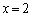 �Ƃ��āAa�́A
�Ƃ��āAa�́A ������A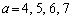 �̂Ƃ��ɁA
�̂Ƃ��ɁA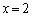 ��(��)�̉��ɂȂ�܂��B
��(��)�̉��ɂȂ�܂��B
����ŁA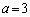 ���c��܂����A���̂Ƃ��@�́A
���c��܂����A���̂Ƃ��@�́A �����̕s��������x�́A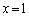 �݂̂ł����A����͉E���̕s�����������A
�݂̂ł����A����͉E���̕s�����������A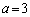 �̂Ƃ��ɂ́A(��)�̉��͑��݂��܂���B
�̂Ƃ��ɂ́A(��)�̉��͑��݂��܂���B
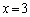 �����ɂȂ�Ƃ��A�@��
�����ɂȂ�Ƃ��A�@��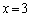 �Ƃ��āAa�́A
�Ƃ��āAa�́A 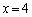 �����ɂȂ�Ƃ��A�@��
�����ɂȂ�Ƃ��A�@��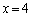 �Ƃ��āAa�́A
�Ƃ��āAa�́A������A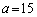 �̂Ƃ��ɁA(��)����������x�͑��݂����A(��)�͉��������܂���B
�̂Ƃ��ɁA(��)����������x�͑��݂����A(��)�͉��������܂���B
�]���āA(1)�̌��ʂ�����āA(��)�����������Ȃ��悤��a�����������ɕ��ׂ�ƁA �ƂȂ�܂��B
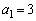 �C
�C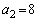 ......[��]
......[��]
(3) (2)�ŇA�̂悤�ɂȂ�̂́A�@��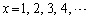 �Ƃ����Ƃ��ɓ�����s�����A
�Ƃ����Ƃ��ɓ�����s�����A �̂����ꂩ����������a�̏W��
����A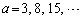 ���R��邩��ł��B�R��鐳�������e�s�����̉E�ӂɏo�Ă��鐮���l�ɂȂ��Ă��邱�Ƃɒ��ӂ���ƁA�@�̉E��
���R��邩��ł��B�R��鐳�������e�s�����̉E�ӂɏo�Ă��鐮���l�ɂȂ��Ă��邱�Ƃɒ��ӂ���ƁA�@�̉E��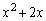 ��x��1���珇�ɓ���ē����鐮���l��a���Ƃ�Ƃ��A�܂�An�𐳐����Ƃ��āA
��x��1���珇�ɓ���ē����鐮���l��a���Ƃ�Ƃ��A�܂�An�𐳐����Ƃ��āA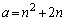 �̂Ƃ��ɁA(��)�̉������݂��Ȃ����Ƃ��A�\���ł��܂��B
�̂Ƃ��ɁA(��)�̉������݂��Ȃ����Ƃ��A�\���ł��܂��B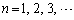 �Ƃ��āA
�Ƃ��āA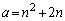 �̂Ƃ��@�́A
�̂Ƃ��@�́A 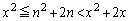 �@����B
�@����B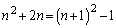 �C
�C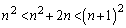 ���A�B�̍����̕s�����������̐���x�́A
���A�B�̍����̕s�����������̐���x�́A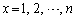 �ł����A���̑S�Ă��B�̉E���̕s���������܂���B����āA
�ł����A���̑S�Ă��B�̉E���̕s���������܂���B����āA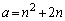 �̂Ƃ��A(��)�̉��͑��݂��܂���B
�̂Ƃ��A(��)�̉��͑��݂��܂���B
�܂��A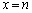 �����ɂȂ�Ƃ��A�@��
�����ɂȂ�Ƃ��A�@��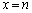 �Ƃ��āA
�Ƃ��āA���Aa�́A
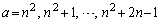 �@����C
�@����C�ƂȂ�܂����Aa���C�̂����ꂩ�ł���A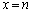 �̂Ƃ��A
�̂Ƃ��A �����藧�̂ŁA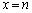 �͇@�����A(��)�͉��������܂��B
�͇@�����A(��)�͉��������܂��B
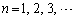 �Ƃ��āA
�Ƃ��āA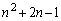 ��
��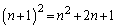 �̊Ԃɂ́A��������
�̊Ԃɂ́A��������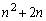 �����Ȃ��̂ŁA������a��
�����Ȃ��̂ŁA������a��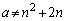 (
(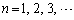 )�ƂȂ�Ƃ��ɂ́A(��)�͉��������܂��B
)�ƂȂ�Ƃ��ɂ́A(��)�͉��������܂��B
�ȏ���A 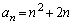 �@(
�@(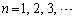 )
)�ł��B
�� 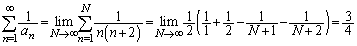 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���H�吔�wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B