���H�吔�w'10�N�O��[4]
a�𐳂̒萔�Ƃ���B���_��O�Ƃ�����W���ʏ�ɒ�_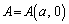 �ƁAA�ƈقȂ铮�_
�ƁAA�ƈقȂ铮�_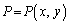 ���Ƃ�B���̏���
���Ƃ�B���̏���
A����P�Ɍ�������������̓_Q�ɑ�
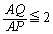 �Ȃ��
�Ȃ�� 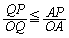
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�ȉ��ł́A��蕶����P���������ׂ������Ƃ��ďo�Ă��������𖽑�C�ƌĂԂ��Ƃɂ��܂��B���́g����C�F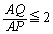 �Ȃ��
�Ȃ�� 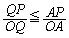 �h�̈Ӗ�����Ƃ��낪�킩��ɂ��������łȂ��A�_���I�ɓ���g��ł����ɁA����=0�̍l�����K�v�ŁA��H�����]�Ȑ܂������܂��B
�h�̈Ӗ�����Ƃ��낪�킩��ɂ��������łȂ��A�_���I�ɓ���g��ł����ɁA����=0�̍l�����K�v�ŁA��H�����]�Ȑ܂������܂��B
�܂��́A�ȒP�ȏꍇ�����ӂ����ނ悤�ɂ��܂��傤�B
�����Ȃ���W���ʏ�ōl����̂ł͓���̂ŁAx�����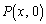 �C
�C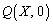 ���Ƃ��Ē��ׂĂ݂܂��B
���Ƃ��Ē��ׂĂ݂܂��B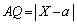 �C
�C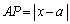 �C
�C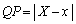 �C
�C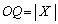 �C
�C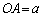 �C�܂��AP��A�ƈقȂ�̂�
�C�܂��AP��A�ƈقȂ�̂�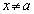 �ł���AQ�́AA����P�Ɍ�������������̓_�Ȃ̂ŁA
�ł���AQ�́AA����P�Ɍ�������������̓_�Ȃ̂ŁA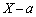 ��0�ɂȂ邱�Ƃ��܂߂�
��0�ɂȂ邱�Ƃ��܂߂�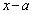 �Ɠ������ł��B
�Ɠ������ł��B
����C�́A
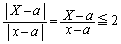 �Ȃ��
�Ȃ�� 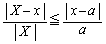 �@����@
�@����@
�@��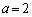 �C
�C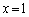 �Ƃ��Ă݂�ƁA
�Ƃ��Ă݂�ƁA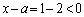 �Ȃ̂�
�Ȃ̂�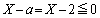 �ł����āA
�ł����āA
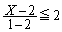 �Ȃ��
�Ȃ�� 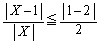
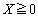 �Ȃ��
�Ȃ�� 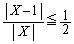
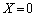 �̂Ƃ��ɁA
�̂Ƃ��ɁA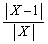 �̕��ꂪ0�ɂȂ��Ă��܂��̂ŁA
�̕��ꂪ0�ɂȂ��Ă��܂��̂ŁA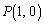 �͖���C�������A
�͖���C�������A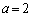 �̂Ƃ�
�̂Ƃ�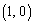 �͗̈�D���̓_�ł͂���܂���B
�͗̈�D���̓_�ł͂���܂���B
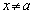 ���A�@��
���A�@��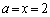 �Ƃ��邱�Ƃ͂ł��܂���B
�Ƃ��邱�Ƃ͂ł��܂���B
�@��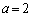 �C
�C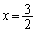 �Ƃ��Ă݂�ƁA
�Ƃ��Ă݂�ƁA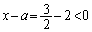 �Ȃ̂�
�Ȃ̂�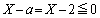 �ł����āA
�ł����āA
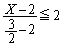 �Ȃ��
�Ȃ�� 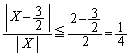
���A���ǁA
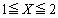 �Ȃ��
�Ȃ�� 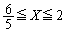
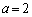 �̂Ƃ�
�̂Ƃ�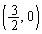 ���̈�D���̓_�ł͂���܂���B
���̈�D���̓_�ł͂���܂���B
�@��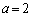 �C
�C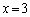 �Ƃ��Ă݂�ƁA
�Ƃ��Ă݂�ƁA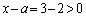 �Ȃ̂�
�Ȃ̂�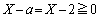 �ł����āA
�ł����āA
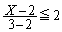 �Ȃ��
�Ȃ�� 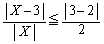
���A
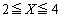 �Ȃ��
�Ȃ�� 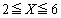
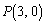 �͖���C�����A
�͖���C�����A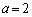 �̂Ƃ�
�̂Ƃ�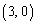 �͗̈�D���̓_�ł��B
�͗̈�D���̓_�ł��B
������ł��Aa�Cx�ɂ��낢��Ȓl�����āA����C����������ꍇ�A�������Ȃ��ꍇ�������Ă݂邱�ƂɂȂ�ł��傤�B
�����ŁA���l������Ă���Ă݂����Ƃ����܂��B����C�̏\�������F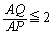 ���瓾����Q�̍��W�Ɋւ���s�����͈̔͂�
���瓾����Q�̍��W�Ɋւ���s�����͈̔͂�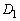 �C�K�v�����F
�C�K�v�����F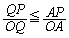 ���瓾����Q�̍��W�Ɋւ���s�����͈̔͂�
���瓾����Q�̍��W�Ɋւ���s�����͈̔͂�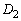 �Ƃ��āA������_
�Ƃ��āA������_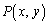 �ɂ��āA
�ɂ��āA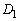 ��
��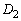 �Ɋ܂܂�Ă���Ζ���C����������̂Łu
�Ɋ܂܂�Ă���Ζ���C����������̂Łu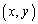 �͗̈�D���̓_���v�Ɣ��f���A
�͗̈�D���̓_���v�Ɣ��f���A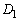 ��
��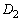 �Ɋ܂܂�Ă��Ȃ���Ζ���C���������Ȃ��̂Łu
�Ɋ܂܂�Ă��Ȃ���Ζ���C���������Ȃ��̂Łu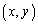 �͗̈�D���̓_�ł͂Ȃ��v�Ɣ��f���Ă��܂��B
�͗̈�D���̓_�ł͂Ȃ��v�Ɣ��f���Ă��܂��B
�ł���A��ʓI���_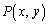 �ɂ��āA�\���������瓾����͈͂��A�K�v�������瓾����͈͂Ɋ܂܂��悤��
�ɂ��āA�\���������瓾����͈͂��A�K�v�������瓾����͈͂Ɋ܂܂��悤��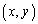 �ׂ�A�u����C����������v�Ƃ�����������P����Ȃ�̈�D�����߂���͂��ł��B
�ׂ�A�u����C����������v�Ƃ�����������P����Ȃ�̈�D�����߂���͂��ł��B
�����ł́A�K�v�����A�\�������͈̔͂��l���₷�����邽�߂ɁA
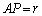 �C
�C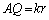
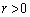 �CQ�͔�����AP��̓_�Ȃ̂�
�CQ�͔�����AP��̓_�Ȃ̂�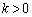 �ł��B�܂��A������AP��x���������ƂȂ��p��θ (
�ł��B�܂��A������AP��x���������ƂȂ��p��θ (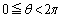 )�Ƃ��܂��B
)�Ƃ��܂��B
P�̍��W��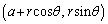 �CQ�̍��W��
�CQ�̍��W��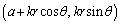 �ƂȂ�܂��B
�ƂȂ�܂��B
����ɁA����C�̕K�v�����̕����OQ���o�Ă���̂ŁAQ��O�ƈ�v���܂���B
Q��O�ƈ�v����Ƃ��AQ�̍��W�ɂ��āA
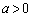 �C
�C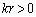 �Ȃ̂ŁA
�Ȃ̂ŁA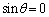 �C
�C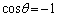 �C�܂�A
�C�܂�A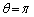
�܂��A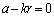 ���
���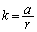
k�͔C�ӂ̐����l���Ƃ蓾�Ă��܂��̂ŁAP�̈ʒu�ɂ����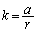 �ƂȂ�\����r�����邱�Ƃ͂ł��Ȃ��̂ŁA
�ƂȂ�\����r�����邱�Ƃ͂ł��Ȃ��̂ŁA
P�����݂���̈�D�́A
�ƂȂ�͈͂��܂�ł��Ă͂Ȃ�Ȃ��@���(��)
�Ƃ������Ƃɒ��ӂ��܂��B
���āA����C�̏\�������F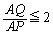 ���A
���A
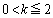 �@����A
�@����A
����C�̕K�v�����F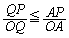 ���A
���A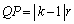 �C
�C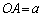 ��p���āA
��p���āA
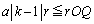 �@����B
�@����B
�B�̗��ӂ́A���ɂȂ邱�Ƃ͂Ȃ��Ar�Ŋ����āA���ӂ�2�悷��ƁA
��������ƁA
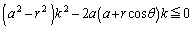 �@����C
�@����C(i) 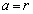 �̂Ƃ��A�_P��A�𒆐S�Ƃ��锼�aa�̉~����̓_�ł����A�C���A
�̂Ƃ��A�_P��A�𒆐S�Ƃ��锼�aa�̉~����̓_�ł����A�C���A 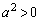 ���A
���A(��)���l������ƁA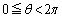 �ɂ�����
�ɂ�����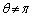 �ł����
�ł����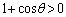 �Ȃ̂ŁA
�Ȃ̂ŁA 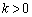 �@����D
�@����D(��)���A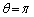 �̂Ƃ��AP��
�̂Ƃ��AP��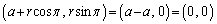 �ɗ���̂ŁA�̈�D����
�ɗ���̂ŁA�̈�D����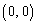 �͏�����܂��B
�͏�����܂��B
����āA���̂Ƃ��A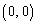 �������āA�g�A �Ȃ�� �D�h�͐������A����C���������܂��B
�������āA�g�A �Ȃ�� �D�h�͐������A����C���������܂��B (ii) 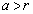 �̂Ƃ��A�_P��A�𒆐S�Ƃ��锼�aa�̉~���������̓_�ł����A�C���A
�̂Ƃ��A�_P��A�𒆐S�Ƃ��锼�aa�̉~���������̓_�ł����A�C���A 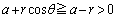 ���A
���A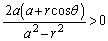 �Ȃ̂ŁA
�Ȃ̂ŁA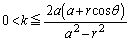 �@����E
�@����E���̂Ƃ��A�g�A �Ȃ�� �E�h (�E�͈̔͂��A�͈̔͂��܂�)���������邽�߂ɁA
�łȂ���Ȃ�܂���B������Đ�������ƁA
�����ŁA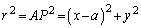 �C
�C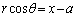 ���A
���A �� 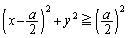 �@����F
�@����F
�܂��A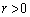 (P��A�ƈقȂ�_)�ɒ��ӂ���ƁA
(P��A�ƈقȂ�_)�ɒ��ӂ���ƁA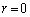 �� �g
�� �g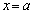 ����
���� 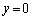 �h���
�h���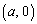 �͏�����܂��B(��)���������܂��B
�͏�����܂��B(��)���������܂��B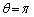 �̂Ƃ��AP
�̂Ƃ��AP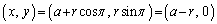 �́Ax�����
�́Ax�����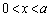 �̕������܂��B���̕����͗̈�D���珜�����ׂ��ł����A���������F�Ɋ܂܂�Ă��܂���B
�̕������܂��B���̕����͗̈�D���珜�����ׂ��ł����A���������F�Ɋ܂܂�Ă��܂���B
����āA���̂Ƃ��́A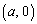 �������̈�F���ɑ��݂���P�ɂ��āA�g�A �Ȃ�� �E�h���������A����C���������܂��B
�������̈�F���ɑ��݂���P�ɂ��āA�g�A �Ȃ�� �E�h���������A����C���������܂��B (iii) 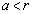 �̂Ƃ��A�_P��A�𒆐S�Ƃ��锼�aa�̉~�����O���̓_�ł����A�C���A
�̂Ƃ��A�_P��A�𒆐S�Ƃ��锼�aa�̉~�����O���̓_�ł����A�C���A 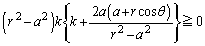 �@����G
�@����GP��x���W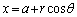 �ɂ��āA(a)
�ɂ��āA(a) 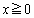 �̂Ƃ��A�G�̒��J�b�R���͐��ŁA�s�����G����k�́A
�̂Ƃ��A�G�̒��J�b�R���͐��ŁA�s�����G����k�́A 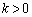 �@����D
�@����D
���̂Ƃ��A�g�A �Ȃ�� �D�h���������܂��B(b) 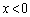 �̂Ƃ��A
�̂Ƃ��A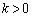 ���A�s�����G����k�́A
���A�s�����G����k�́A 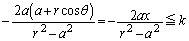 �@����H
�@����H
�A����k�̂����A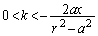 �ƂȂ�k�͇H�������A�g�A �Ȃ�� �H�h�͐������܂���B
�ƂȂ�k�͇H�������A�g�A �Ȃ�� �H�h�͐������܂���B(a)�C(b)���A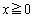 �ł��B(��)���������܂��B
�ł��B(��)���������܂��B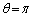 �̂Ƃ��AP
�̂Ƃ��AP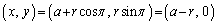 �́Ax�����
�́Ax�����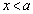 �̕������܂����A���̕����͂�������
�̕������܂����A���̕����͂�������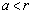 ����
����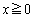 �̕����ɂ͊܂܂�Ă��܂���B
�̕����ɂ͊܂܂�Ă��܂���B
����āA���̂Ƃ��́A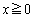 �ɂ����āA�g�A �Ȃ�� �D�h���������A����C���������܂��B
�ɂ����āA�g�A �Ȃ�� �D�h���������A����C���������܂��B
 (i)�C(ii)�C(iii)���܂Ƃ߂�ƁA����C����������̂́A
(i)�C(ii)�C(iii)���܂Ƃ߂�ƁA����C����������̂́A
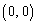 ������
������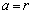 �C�܂��́A
�C�܂��́A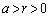 ����
���� 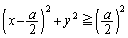 (
(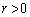 ���
���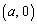 ������)�C�܂��́A
������)�C�܂��́A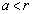 ����
���� 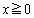
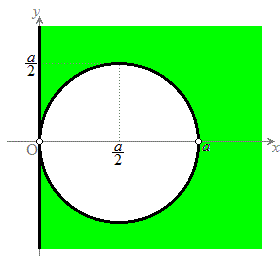
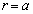 ��A�𒆐S�Ƃ��锼�aa�̉~����\�����Ƃɒ��ӂ��āA��������ƁA�̈�D�́A
��A�𒆐S�Ƃ��锼�aa�̉~����\�����Ƃɒ��ӂ��āA��������ƁA�̈�D�́A
�ł����āA�}������ƉE�}���ΐF���F��(���E�����܂ݔ��}��������)�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���H�吔�wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B