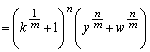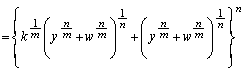���H�吔�w'90�N�O��[1]
x�Cy�Cz�Cw�𐳐��Ƃ���B�C�ӂ̐��̐���m�Cn�ɑ��āA
�����藧���߂̕K�v�\�����������߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@���������u�ԁA����������������A�ƁA�����������ł��܂������Ȗ��ł��B�������ł��A�ŏ��̐����A��R�Ɨ����s���������A���邢�́A�����Ɏ��̖��ɔ��ł��܂������m��܂���B�ł����A���w�����͋����ł��B���Ƃ��Ă��A���̖��ɐH�������낤�A�ƁA�v���̂ł���A�܂��́A1�_�ł��ǂ�����A���_����悹���悤�Ƃ������z�ɗ��ׂ��ł��B
�������A���̖������Ă����Ė��Ӗ��Ȃ��Ƃ������Ă��A���_�ł���킯�ł͂���܂���B
���̖����l����̂ɂȂ���悤�Ȃ��ƂŎ肪��������ޕK�v������܂��B
���̖�肪�A�Ȃ��A�����Ɏ肪���Ȃ����ƌ����ƁAn�悳��Ă���Ƃ��낪����A�W�J���ē藝�Ȃǂ��g���̂ł́A�b���c��ɂȂ��Ă��܂�����ł��B
�ł���A�܂��́A�肪���₷���悤�ɁAm��n�ɂ킩��₷�������Ȏ��R����������Ƃ��납��n�߂邱�Ƃɂ��܂��B
m�Cn�� �������Ă݂�ƁA�^���͗��ӂƂ�
�������Ă݂�ƁA�^���͗��ӂƂ�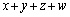 �ƂȂ�̂Ő������܂��B
�ƂȂ�̂Ő������܂��B
����������A���ėp���ɂ́A���̎��������ł������Ă����悤�ɂ��܂��傤�B������O�̂悤�Ȃ��Ƃł����A���̖��̐��������Ⴏ��A����������ƁA1�_���炢�͂��炦�邩���m��܂���B����1�_�œ�����������Ă��܂��̂��Ƃ�����A���������ꂾ���̂��Ƃő傫��1�_�ł��B
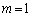 �C
�C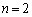 �������Ă݂�ƁA�^���́A
�������Ă݂�ƁA�^���́A
��������ƁA
���ӂ�2�悷��ƁA
�ƂȂ�A
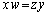 �@����@
�@����@
�����܂œ��Ăɏ����Ă����A2�C3�_�A�^���ǂ����5�_���炢���҂ł��邩���m��܂���B�A���A���ꂾ���ł́A�K�v�����Ƃ����������\�����̊m�F���ł��Ă��܂���B�܂�A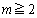 �C���邢�́A
�C���邢�́A �̏ꍇ�ɂ����藧���ǂ����A�m�F����Ă��܂���B��ʓI�ȏꍇ�ɂ��Ă����藧�̂��ǂ����m�F���邱�Ƃɂ��܂��B
�̏ꍇ�ɂ����藧���ǂ����A�m�F����Ă��܂���B��ʓI�ȏꍇ�ɂ��Ă����藧�̂��ǂ����m�F���邱�Ƃɂ��܂��B
�t�ɁA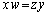 �̂Ƃ��A
�̂Ƃ��A
�E �̂Ƃ��́A�^���́A���ӁA�E�ӂƂ��A
�̂Ƃ��́A�^���́A���ӁA�E�ӂƂ��A �ƂȂ�A�^���͐������܂��B
�ƂȂ�A�^���͐������܂��B �E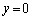 ����
����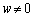 �̂Ƃ��́A�@���
�̂Ƃ��́A�@���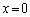 �ł��B���̂Ƃ��A�^���́A���ӁA�E�ӂƂ��A
�ł��B���̂Ƃ��A�^���́A���ӁA�E�ӂƂ��A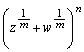 �ƂȂ�A�^���͐������܂��B
�ƂȂ�A�^���͐������܂��B �E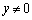 ����
����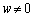 �̂Ƃ��́A�@��
�̂Ƃ��́A�@��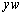 �Ŋ���A
�Ŋ���A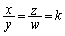 �Ƃ����ƁA�^�����ӂ́A
�Ƃ����ƁA�^�����ӂ́A �^���E�ӂ́A
�ƂȂ�A�^���͐������܂��B
�ȏ���A���߂��K�v�\�������́A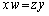 ......[��]
......[��]
��U�s���̌��S�ȏ邾�Ǝv���Ă�����肪�Am�Cn�ɂ�����Ɛ��l������邾���ł������Ȃ������Ă��܂��A�Ƃ����v�̂ɓ���Ă����Ē��������Ǝv���܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���H�吔�wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 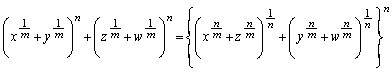
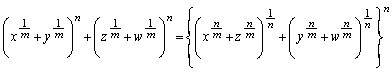
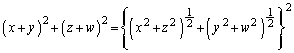
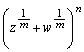 �ƂȂ�A�^���͐������܂��B
�ƂȂ�A�^���͐������܂��B