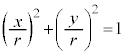三角比の拡張 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
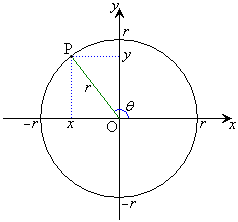 右図の、原点Oを中心とする半径rの円周上の点P
右図の、原点Oを中心とする半径rの円周上の点P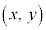 に対して、角θ はx軸から反時計回りに線分OPまで回転した角とする(
に対して、角θ はx軸から反時計回りに線分OPまで回転した角とする(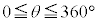 )。
)。
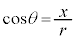 ,
,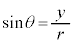 ,
,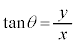 (
(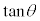 では
では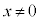 )
)
この定義の仕方で、直角三角形による三角比の定義(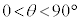 )と矛盾はありません。
)と矛盾はありません。
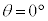 のとき、
のとき、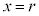 ,
,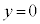 より、
より、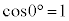 ,
,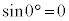 ,
,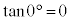
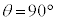 のとき、
のとき、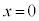 ,
,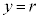 より、
より、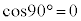 ,
,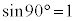 ですが、分母が0になるため、
ですが、分母が0になるため、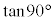 は定義できません。
は定義できません。
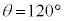 のとき、
のとき、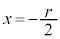 ,
,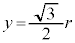 より、
より、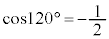 ,
,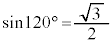 ,
,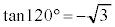
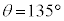 のとき、
のとき、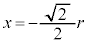 ,
,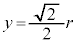 より、
より、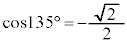 ,
,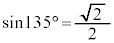 ,
,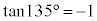
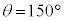 のとき、
のとき、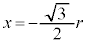 ,
,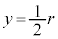 より、
より、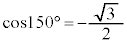 ,
,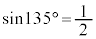 ,
,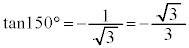
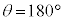 のとき、
のとき、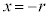 ,
,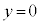 より、
より、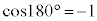 ,
,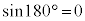 ,
,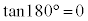
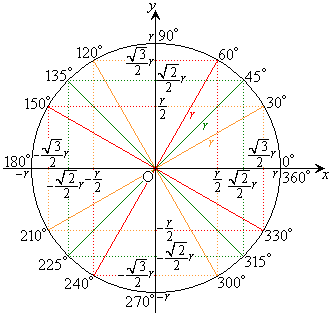 余弦
余弦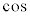 の正負は円周上の点のx座標で決まります。θ が第1象限の角では
の正負は円周上の点のx座標で決まります。θ が第1象限の角では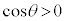 ,第2象限の角では
,第2象限の角では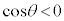 ,第3象限の角では
,第3象限の角では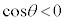 ,第4象限の角では
,第4象限の角では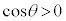
正弦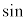 の正負は円周上の点のy座標で決まります。θ が第1象限の角では
の正負は円周上の点のy座標で決まります。θ が第1象限の角では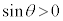 ,第2象限の角では
,第2象限の角では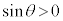 ,第3象限の角では
,第3象限の角では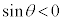 ,第4象限の角では
,第4象限の角では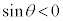
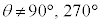 のとき、
のとき、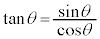 が成り立ちます。
が成り立ちます。
また、原点Oを中心とする半径rの円周上の点P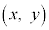 では、
では、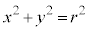 が成立します。
が成立します。
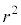 で割って、
で割って、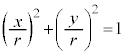
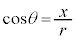 ,
,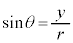 より、が成立します。
より、が成立します。
さらに、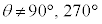 のとき、
のとき、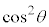 で割ると、が成立します。
で割ると、が成立します。
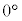 から
から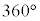 までのさまざまな角に対する三角比の値を以下の表に示します。
までのさまざまな角に対する三角比の値を以下の表に示します。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。