���啶�n���w'09�N[1]
���W���ʂɂ����Č��_�𒆐S�Ƃ��锼�a2�̉~��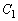 �Ƃ��A�_
�Ƃ��A�_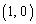 �𒆐S�Ƃ��锼�a1�̉~��
�𒆐S�Ƃ��锼�a1�̉~��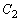 �Ƃ���B�܂��A�_
�Ƃ���B�܂��A�_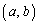 �𒆐S�Ƃ��锼�at �̉~
�𒆐S�Ƃ��锼�at �̉~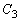 ���A
���A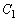 �ɓ��ڂ��A����
�ɓ��ڂ��A����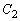 �ɊO�ڂ���Ɖ��肷��B�������Ab�͐��̒萔�Ƃ���B
�ɊO�ڂ���Ɖ��肷��B�������Ab�͐��̒萔�Ƃ���B
(1) a�Cb��t ��p���ĕ\���B�܂��At ���Ƃ蓾��l�͈̔͂����߂�B
(2) t��(1)�ŋ��߂��͈͂��Ƃ��Ab�̍ő�l�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@(1)�́A2�~�̈ʒu�W�Ɋւ�����ł��B�}�`�I�Ӗ����l����悤�ɂ��܂��傤�B(2)��2�����̍ő�ŏ��̖��ł��B
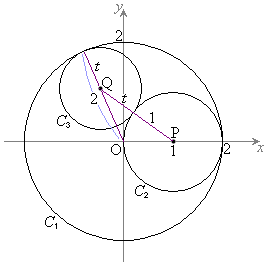 (1) 2�~���ڂ���Ƃ��A2�~�̒��S�͐ړ_�ƈ꒼����ɂ���܂��B
(1) 2�~���ڂ���Ƃ��A2�~�̒��S�͐ړ_�ƈ꒼����ɂ���܂��BP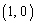 �CQ
�CQ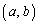 �Ƃ���ƁA
�Ƃ���ƁA
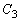 ��
��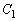 �ɓ��ڂ���̂ŁA2�~�̒��S�ԋ���OQ�͔��a�̍��ɓ������A
�ɓ��ڂ���̂ŁA2�~�̒��S�ԋ���OQ�͔��a�̍��ɓ������A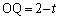
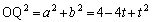 �@����@
�@����@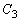 ��
��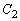 �ɊO�ڂ���̂ŁA2�~�̒��S�ԋ���PQ�͔��a�̘a�ɓ������A
�ɊO�ڂ���̂ŁA2�~�̒��S�ԋ���PQ�͔��a�̘a�ɓ������A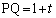
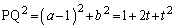 �@����A
�@����A�@�|�A���A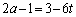
�� 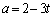 ......[��]�@���A
......[��]�@���A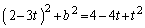
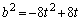 �@����B
�@����B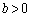 ���A
���A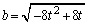 ......[��]�܂��A
......[��]�܂��A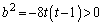
�� 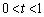 ......[��]
......[��]���D�~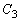 �̒��S��x��������ɂ���(
�̒��S��x��������ɂ���(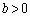 )�Ƃ��A�~
)�Ƃ��A�~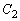 �̔��at�́AQ��
�̔��at�́AQ��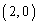 �ɋ߂Â��Ƃ�����ł�0�ɋ߂Â��AQ��
�ɋ߂Â��Ƃ�����ł�0�ɋ߂Â��AQ��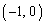 �ɋ߂Â��Ƃ�����ł�1�ɋ߂Â��̂ŁA
�ɋ߂Â��Ƃ�����ł�1�ɋ߂Â��̂ŁA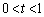 �ł��B
�ł��B
(2) �B���A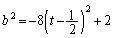
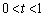 �ɂ����āA
�ɂ����āA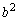 ��
��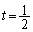 �̂Ƃ��ő�l2���Ƃ�̂ŁAb�̍ő�l��
�̂Ƃ��ő�l2���Ƃ�̂ŁAb�̍ő�l��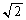 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B