線積分
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
平面上の曲線C: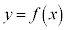 の
の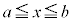 の部分の長さsを考えます。
の部分の長さsを考えます。
まず、この曲線の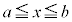 の部分をn等分して、その一つ分をほぼ長さ
の部分をn等分して、その一つ分をほぼ長さ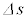 の線分であると見なし、その線分を対角線とする長方形を考えます。長方形の各辺は、x軸,y軸に平行とし、x軸に平行な辺の長さが
の線分であると見なし、その線分を対角線とする長方形を考えます。長方形の各辺は、x軸,y軸に平行とし、x軸に平行な辺の長さが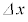 ,y軸に平行な辺の長さが
,y軸に平行な辺の長さが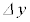 だとします。
だとします。
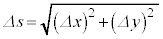 ,
,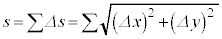
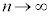 の極限で、
の極限で、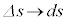 ,
,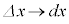 ,
,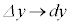 とすると、
とすると、
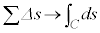 ,
,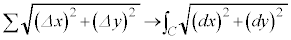
ここで、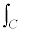 は、経路Cに沿って積分するという意味です。
は、経路Cに沿って積分するという意味です。
よって、曲線に沿った微小な長さを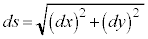 として、曲線の長さsは、
として、曲線の長さsは、
で与えられます。
曲線C上で経路に沿った長さsの関数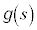 の経路に沿った積分
の経路に沿った積分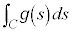 は、
は、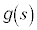 をxの関数として表したとき
をxの関数として表したとき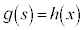 として、
として、
この積分をスカラー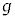 の線積分と言います。
の線積分と言います。
曲線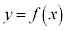 の接線がx軸となす角をθ とすると、
の接線がx軸となす角をθ とすると、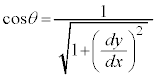 なので、
なので、
とも書けます。
曲線Cの接線方向の単位ベクトルを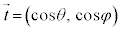 (θ は
(θ は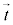 とx軸,φは
とx軸,φは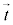 とy軸のなす角),ベクトル
とy軸のなす角),ベクトル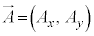 の成分
の成分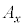 がxの関数、
がxの関数、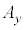 がyの関数だとして、
がyの関数だとして、
より、
この積分をベクトル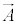 の線積分と言います。当ウェブサイトでは、
の線積分と言います。当ウェブサイトでは、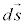 を線素と呼ぶことにします。
を線素と呼ぶことにします。
経路Cが特に閉曲線である場合には、線積分を、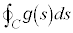 ,
,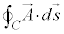 のように書きます。
のように書きます。
空間中の曲線Cについても、同様の議論によって、曲線の長さを
曲線Cの接線方向の単位ベクトルを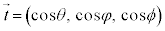 ,線素を
,線素を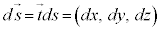 として、ベクトル
として、ベクトル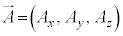 の線積分を
の線積分を
と考えます。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
物理基礎事項TOP 物理TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 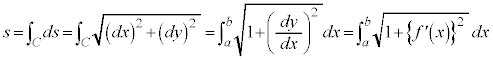
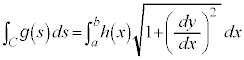
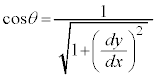 なので、
なので、