�ʐϕ��@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
��ԓ��̂���Ȗ�U��Œ�`����A�Ȗ�U��̓_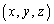 �ɂ�����l��
�ɂ�����l��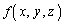 �ŗ^����������������Ƃ��܂��B
�ŗ^����������������Ƃ��܂��B
�Ȗ�U��̓_���A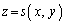 �C
�C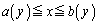 �C
�C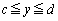 �����Ă���(����ȊO�̏ꍇ�́A�����ƕ��G�ɂȂ�܂�)�Ƃ��܂��B
�����Ă���(����ȊO�̏ꍇ�́A�����ƕ��G�ɂȂ�܂�)�Ƃ��܂��B
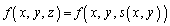 �́Ax�Cy�̊��ł��B
�́Ax�Cy�̊��ł��B
y���Œ肵�A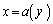 ����
����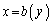 �܂ŁAx�ɂ��āA
�܂ŁAx�ɂ��āA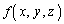 ��ϕ����܂��B
��ϕ����܂��B
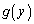 ��y�̊��ł��B
��y�̊��ł��B
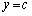 ����
����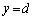 �܂ŁAy�ɂ��āA
�܂ŁAy�ɂ��āA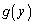 ��ϕ��������́A
��ϕ��������́A
���A
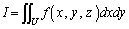 �@����@
�@����@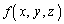 �̋Ȗ�U�ɂ������ʐϕ��ƌ����܂��B
�̋Ȗ�U�ɂ������ʐϕ��ƌ����܂��B
�_P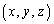 �ɂ�����Ȗ�U�̐ڕ��ʂ�K�Ƃ��܂��B
�ɂ�����Ȗ�U�̐ڕ��ʂ�K�Ƃ��܂��B
�_P��ʂ�xy���ʂɐ�������x���ɕ��s�ȕ��ʂ�K���ƁA����ɂł���Ȑ��̐ڐ��̕����x�N�g����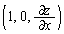 �ł��B
�ł��B
�_P��ʂ�xy���ʂɐ�������y���ɕ��s�ȕ��ʂ�K���ƁA����ɂł���Ȑ��̐ڐ��̕����x�N�g����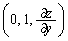 �ł��B
�ł��B
�ڕ���K�̖@���x�N�g���́A����2�̃x�N�g������镽�ʂɐ����ȃx�N�g���Ȃ̂ŁA���҂̊O�ς����߂�ƁA
���̃x�N�g���̑傫���́A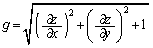 �ƂȂ�̂ŁA�ڕ��ʂ̖@���x�N�g��
�ƂȂ�̂ŁA�ڕ��ʂ̖@���x�N�g��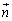 ��x���Cy���Cz���ƂȂ��p��θ�Cφ�Cϕ�Ƃ��āA
��x���Cy���Cz���ƂȂ��p��θ�Cφ�Cϕ�Ƃ��āA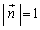 �����悤�ɂ���ƁA
�����悤�ɂ���ƁA
�ł��B
�ڕ���K��ɂƂ�����������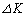 �̖ʐς�
�̖ʐς�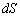 �C
�C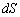 ��xy���ʂւ̐��ˉe��
��xy���ʂւ̐��ˉe��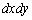 ���Ƃ��āA
���Ƃ��āA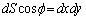 �ł�(���l�ɁA
�ł�(���l�ɁA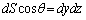 �C
�C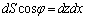 )�B
)�B
�@�ɂ����āA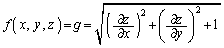 �̂Ƃ��A�܂�A
�̂Ƃ��A�܂�A
�́A�Ȗ�U�̖ʐ���\���܂��B
�܂��A��L���A�ʐϕ����A
�Ə������Ƃ��ł��܂��B���l�ɂ��āA
���l���邱�Ƃ��ł��܂��B
�Ȗ�U��Œ�`����A�Ȗ�U��̓_P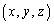 �ɂ����ăx�N�g���l
�ɂ����ăx�N�g���l
���Ƃ�����l���܂��B
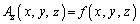 �ƌ��āA��L�̖ʐϕ�I���l����ƁA
�ƌ��āA��L�̖ʐϕ�I���l����ƁA
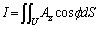 �@����A
�@����A
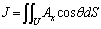 �@����B
�@����B
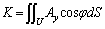 �@����C
�@����C
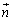 �ƕ��s�A�܂�A�_P�ɂ�����Ȗ�U�̐ڕ���K�Ɛ���(�����͕Ȗʂł͋Ȗʂ̊O���ɏo������Ƃ��܂�)�ő傫����dS�ł���x�N�g��
�ƕ��s�A�܂�A�_P�ɂ�����Ȗ�U�̐ڕ���K�Ɛ���(�����͕Ȗʂł͋Ȗʂ̊O���ɏo������Ƃ��܂�)�ő傫����dS�ł���x�N�g��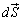 ���l����ƁA
���l����ƁA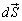 ��x���Cy���Cz���Ƃ̂Ȃ��p���Aθ �Cφ�Cϕ�Ƃ��āA��L���A
��x���Cy���Cz���Ƃ̂Ȃ��p���Aθ �Cφ�Cϕ�Ƃ��āA��L���A
�ł��B����ƁA
�ƂȂ�܂����A����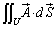 ���x�N�g��
���x�N�g��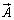 �̋Ȗ�U�ɂ������ʐϕ��ƌ����܂��B����
�̋Ȗ�U�ɂ������ʐϕ��ƌ����܂��B����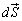 �E�F�u�E�T�C�g�ł́A�ʐϑf���ƌĂԂ��Ƃɂ��܂��B
�E�F�u�E�T�C�g�ł́A�ʐϑf���ƌĂԂ��Ƃɂ��܂��B
�_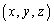 �ɂ����āA�傫����
�ɂ����āA�傫����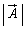 �C������
�C������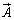 �̌����ƂȂ�悤�ȗ��ꂪ�����āA�B�C�C�C�A��J�CK�CI�́A���̗����x�������Ay�������Az�������̗��ʂ�\���Ă��܂��B
�̌����ƂȂ�悤�ȗ��ꂪ�����āA�B�C�C�C�A��J�CK�CI�́A���̗����x�������Ay�������Az�������̗��ʂ�\���Ă��܂��B
�ʐϕ��F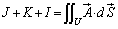 �́A�Ȗ�U��ʂ��ė���o�����ʂ�\���܂��B
�́A�Ȗ�U��ʂ��ė���o�����ʂ�\���܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@������b����TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B