体積分


【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
 【広告】広告はここまでです。
空間内のある領域Vで定義され、領域V内の点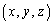における値が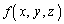で与えられる関数があるとします。
領域Vは、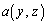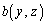，をy，zで決まる関数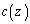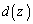，，をzで決まる関数だとして、
，，
を満たす凸な領域だとします(凹んだところがある場合にはもっと複雑です)。
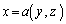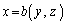y，zを固定し、xについて、からまで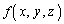を積分します。
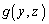は、y，zの関数です。
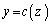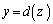zを固定し、yについて、から、まで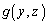を積分します。
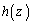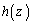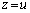は、zの関数です。をから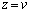まで積分したもの
を、
と書いて、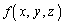の領域Vにおける体積分と言います。
特に、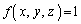の場合、Iは、領域Vの体積になっています。
また、記号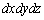を領域内の微小体積と考えて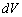と書きます。このdVを当ウェブ・サイトでは、体積素片と呼ぶことにします。
です。


【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
 【広告】広告はここまでです。
　　物理基礎事項TOP　　物理TOP　　TOPページに戻る

【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。
©2005-2024
(有)りるらる
苦学楽学塾 随時入会受付中！
理系大学受験ネット塾苦学楽学塾
(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。