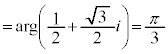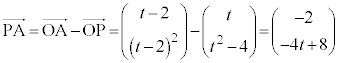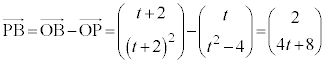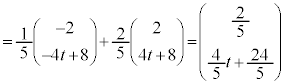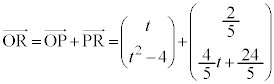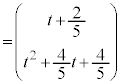慶大理工数学'20年[1]
(1) iを虚数単位とする。複素数平面上で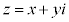 は、
は、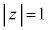 かつ
かつ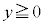 を満たしながら動くとする。ただし、xとyは実数である。このとき、点zのえがく図形をCとする。また、C上に2点
を満たしながら動くとする。ただし、xとyは実数である。このとき、点zのえがく図形をCとする。また、C上に2点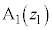 ,
,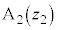 をとったとき、線分
をとったとき、線分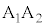 の中点をMとする。
の中点をMとする。
(i) 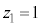 とする。点
とする。点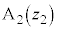 がC上を動くとき、Mのえがく曲線と実軸で囲まれた部分の面積は
がC上を動くとき、Mのえがく曲線と実軸で囲まれた部分の面積は である。
である。
(ii) 2点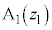 ,
,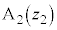 が
が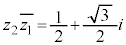 を満たしながらC上を動くとき、Mがえがく曲線の長さは
を満たしながらC上を動くとき、Mがえがく曲線の長さは である。ただし、
である。ただし、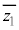 は
は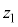 と共役な複素数である。
と共役な複素数である。
(2) 次の2つの放物線
を考える。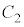 上の点P
上の点P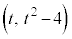 から
から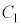 に2本の接線を引く。これら2本の接線と
に2本の接線を引く。これら2本の接線と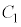 の接点をA,Bとする。ただし、点Aのx座標は点Bのx座標より小さいとする。このとき、点Aのx座標は、tを用いて表すと
の接点をA,Bとする。ただし、点Aのx座標は点Bのx座標より小さいとする。このとき、点Aのx座標は、tを用いて表すと となる。
となる。
次に、線分PAを1:2に内分する点をQ,線分QBを2:3に内分する点をRとする。このとき、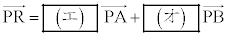 である。点Pが
である。点Pが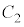 上を動くとき、点R
上を動くとき、点R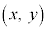 の軌跡の方程式は
の軌跡の方程式は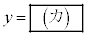 である。
である。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 まずはウォーミング・アップから、という標準的計算問題です。答のみなので、(ア)(イ)は暗算でOKでしょう。
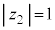 かつ
かつ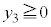 ,より、
,より、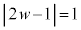 かつ
かつ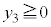 ,つまり、
,つまり、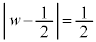 かつ
かつ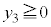
よって、複素数平面上で、Mは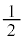 を中心とする半径
を中心とする半径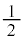 の円のx軸から上の部分を描き、実軸とで囲んでできる図形は、半径
の円のx軸から上の部分を描き、実軸とで囲んでできる図形は、半径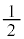 の半円で、その面積は、
の半円で、その面積は、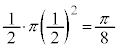 ......[答]
......[答]
 (ii)
(ii) 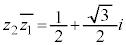 より、
より、よって、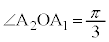 ,また、
,また、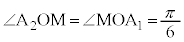 ,
,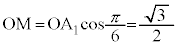 (
(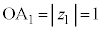 )
)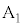 ,
,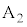 は
は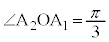 を満たしながら単位円の
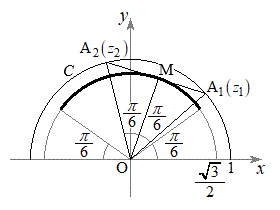
を満たしながら単位円の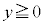 の部分を動くので、Mを表す複素数の偏角をθとして、Mは、原点Oを中心とする半径
の部分を動くので、Mを表す複素数の偏角をθとして、Mは、原点Oを中心とする半径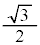 の円の
の円の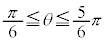 の部分(右図太線、円周の
の部分(右図太線、円周の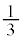 )を描き、その長さは、
)を描き、その長さは、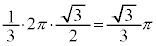 ......[答]
......[答]
接線はP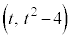 を通るので、
を通るので、 点Aのx座標は小さい方で、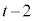 ......[答]点Bのx座標は
......[答]点Bのx座標は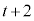 ,Aの座標は
,Aの座標は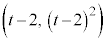 ,Bの座標は
,Bの座標は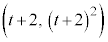 ,
, Qは線分PAを1:2に内分する点、Rは線分QBを2:3に内分する点なので、 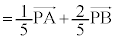 ......[答]
......[答]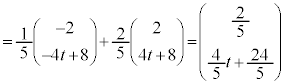
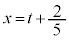 ,
,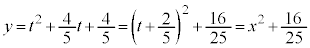 より、点Rの軌跡の方程式は、
より、点Rの軌跡の方程式は、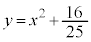 ......[答]
......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
慶大理工数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。