慶應大学理工学部2020年数学入試問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
[1](1) iを虚数単位とする。複素数平面上で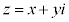
は、
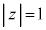かつ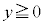
を満たしながら動くとする。ただし、xとyは実数である。このとき、点zのえがく図形をCとする。また、C上に2点
，
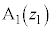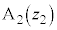をとったとき、線分
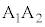の中点をMとする。
(i)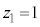 
とする。点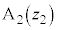
がC上を動くとき、Mのえがく曲線と実軸で囲まれた部分の面積は
である。
(ii) 2点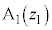
，
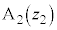が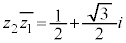
を満たしながらC上を動くとき、Mがえがく曲線の長さは
である。ただし、
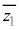は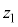
と共役な複素数である。
(2) 次の2つの放物線
を考える。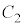
上の点P
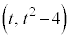から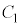
に2本の接線を引く。これら2本の接線と
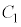の接点をA，Bとする。ただし、点Aのx座標は点Bのx座標より小さいとする。このとき、点Aのx座標は、tを用いて表すと
となる。
次に、線分PAを1：2に内分する点をQ，線分QBを2：3に内分する点をRとする。このとき、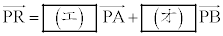
である。点Pが
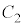上を動くとき、点R
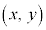の軌跡の方程式は
である。 [解答へ]
[2](1)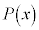 
を整式とし、
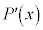を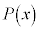
の導関数とする。このとき、
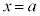が方程式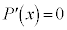
の解となることは、
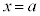が方程式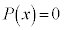
の2重解となるための必要条件であることを証明しなさい。
(2) kが0でない実数を動くとき、放物線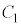
：
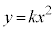と円
：
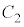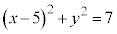の共有点の個数は最大で
個である。
(3) (2)において、放物線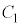
と円
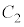の共有点の個数がちょうど1個となるkを考える。このとき、共有点のx座標はkの値によらず
である。また、kの取り得る値は
である。 [解答へ]
[3] 赤い玉と白い玉が3個ずつ入った箱があり、次のような操作を繰り返す。表の出る確率がp，裏の出る確率が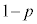
のコインを投げ、
● 表が出た場合、1個の玉を箱から取り出す。
● 裏が出た場合、2個の玉を同時に箱から取り出す。
(1) 
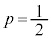とし、各操作で取り出した玉はもとの箱に戻すものとする。2回の操作で取り出した玉の色がすべて赤である確率は
である。 また、3回の操作で取り出した玉の総数が5個であるという条件の下で、取り出した玉の色がすべて赤である確率は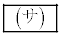
である。
(2) 
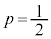とし、各操作で取り出した玉は箱に戻さないものとする。2回の操作で取り出した玉の色がすべて赤である確率は
である。
(3) 
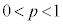とし、各操作で取り出した玉は箱に戻さないものとする。3回の操作で赤い玉と白い玉をちょうど2個ずつ取り出す確率は
である。 また、3回の操作で取り出した赤い玉と白い玉の数が等しい確率が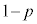
となるのは
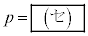のときである。 [解答へ]
[4] 実数全体で定義された連続な関数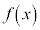
に対し、
とおく。
(1) 
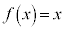のとき、
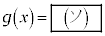である。
(2) 実数全体で定義された連続な関数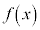
に対し、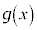
は奇関数であることを示しなさい。
(4) 
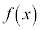が偶関数であり、
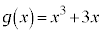となるとき、
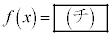である。このとき、
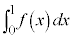の値は
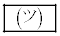である。 [解答へ]
[5] 平行四辺形ABCDにおいて、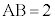
，
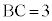とし、対角線ACの長さを4とする。辺AB，BC，CD，DA上にそれぞれ点E，F，G，Hを
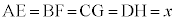を満たすようにとる。ただし、xは
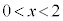の範囲を動くとする。さらに、対角線AC上に点Pを
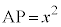を満たすようにとる。以下では、平行四辺形ABCDの面積をSとする。
(1) △AEPの面積を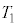
とする。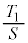
は、xを用いて表すと
となる。
(2) △EFPの面積を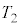
とする。
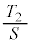は、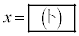
のとき最大値
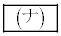をとる。
(3) △GHPの面積を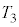
とする。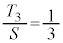
となるのは
のときである。
(4) 点Pが線分EH上にあるのは
のときである。 [解答へ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
慶大理工数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
：
，
：
のとき、
の導関数
を求めると、
である。