�c�嗝�H���w'20�N[4]
�����S�̂Œ�`���ꂽ�A���Ȋ�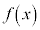 �ɑ��A
�ɑ��A
�Ƃ����B
(1) 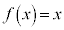 �̂Ƃ��A
�̂Ƃ��A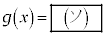 �ł���B
�ł���B
(2) �����S�̂Œ�`���ꂽ�A���Ȋ�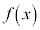 �ɑ��A
�ɑ��A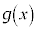 �͊���ł��邱�Ƃ������Ȃ����B
�͊���ł��邱�Ƃ������Ȃ����B
(3) 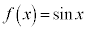 �̂Ƃ��A
�̂Ƃ��A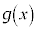 �̓���
�̓���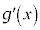 �����߂�ƁA
�����߂�ƁA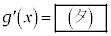 �ł���B
�ł���B
(4) 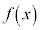 ������ł���A
������ł���A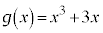 �ƂȂ�Ƃ��A
�ƂȂ�Ƃ��A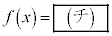 �ł���B���̂Ƃ��A
�ł���B���̂Ƃ��A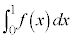 �̒l��
�̒l��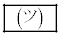 �ł���B
�ł���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�S�c���ϕ��������̖��ł����A����ɏ���ĉ���A�債�����Ƃ͂���܂���B
(1)(�\) 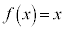 �̂Ƃ��A
�̂Ƃ��A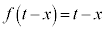
(2) 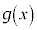 ������ł��邱�Ƃ��������߂ɂ́A
������ł��邱�Ƃ��������߂ɂ́A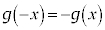 �Ƃ����W���������܂��B��蕶�̎���
�Ƃ����W���������܂��B��蕶�̎���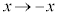 �Ƃ��āA
�Ƃ��āA �����ŁA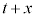 ��
��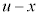 �Ƃ����`�ɂȂ�悤�ɁA
�Ƃ����`�ɂȂ�悤�ɁA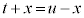 �C�܂�A
�C�܂�A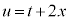 �Ƃ����ƁA
�Ƃ����ƁA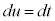 �Ct�F
�Ct�F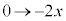 �̂Ƃ�u�F
�̂Ƃ�u�F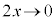 �@(�u���ϕ����Q��)
�@(�u���ϕ����Q��) ����āA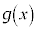 �͊���ł��B
�͊���ł��B
(3)(�^) ��蕶�̎����������Ηǂ��̂ł����A
�Ƃ��Ă��܂��ƁA
����ł́A��ϕ����̒���x��ϕ��̊O�ɒǂ��o�����Ƃ��ł����A�������悤������܂���B
�����ŁA(2)�Œu���ϕ��������Ƃ��āA�����ł��u���ϕ����l���܂��B
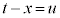 �Ƃ����ƁA
�Ƃ����ƁA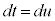 �Ct�F
�Ct�F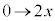 �̂Ƃ��Au�F
�̂Ƃ��Au�F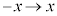
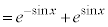 ......[��]
......[��]
(4)(�`) 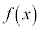 ������A�Ƃ������Ƃ́A
������A�Ƃ������Ƃ́A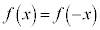 �@����@�@�����藧�A�Ƃ������Ƃł��B�ϕ���
�@����@�@�����藧�A�Ƃ������Ƃł��B�ϕ���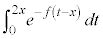 �̂܂܂ł͔�ϕ����̒���x��ϕ��̊O�ɒǂ��o�����Ƃ��ł��Ȃ��̂ŁA(3)�Ɠ������A�u���ϕ����܂��B
�̂܂܂ł͔�ϕ����̒���x��ϕ��̊O�ɒǂ��o�����Ƃ��ł��Ȃ��̂ŁA(3)�Ɠ������A�u���ϕ����܂��B ���ӂƉE�ӂ�x�Ŕ������āA
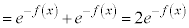 �@(�� �@)
�@(�� �@)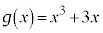 �̂Ƃ��A
�̂Ƃ��A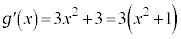 �C����āA
�C����āA
(�c) 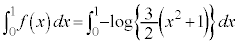
2�Ԗڂ̐ϕ���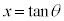 �Ƃ����āA
�Ƃ����āA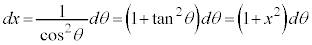 ���A
���A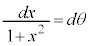 �Cx�F
�Cx�F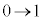 �̂Ƃ��Aθ�F
�̂Ƃ��Aθ�F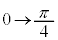
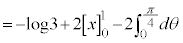
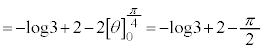 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@�c�嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B