�c�嗝�H���w'20�N[3]
�Ԃ��ʂƔ����ʂ�3����������������A���̂悤�ȑ�����J��Ԃ��B�\�̏o��m����p�C���̏o��m����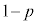 �̃R�C���𓊂��A
�̃R�C���𓊂��A
���@�\���o���ꍇ�A1�̋ʂ�����o���B
���@�����o���ꍇ�A2�̋ʂ��ɔ�������o���B
(1) 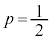 �Ƃ��A�e����Ŏ��o�����ʂ͂��Ƃ̔��ɖ߂����̂Ƃ���B2��̑���Ŏ��o�����ʂ̐F�����ׂĐԂł���m����
�Ƃ��A�e����Ŏ��o�����ʂ͂��Ƃ̔��ɖ߂����̂Ƃ���B2��̑���Ŏ��o�����ʂ̐F�����ׂĐԂł���m���� �ł���B
�ł���B �܂��A3��̑���Ŏ��o�����ʂ̑�����5�ł���Ƃ��������̉��ŁA���o�����ʂ̐F�����ׂĐԂł���m����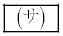 �ł���B
�ł���B
(2) 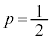 �Ƃ��A�e����Ŏ��o�����ʂ͔��ɖ߂��Ȃ����̂Ƃ���B2��̑���Ŏ��o�����ʂ̐F�����ׂĐԂł���m����
�Ƃ��A�e����Ŏ��o�����ʂ͔��ɖ߂��Ȃ����̂Ƃ���B2��̑���Ŏ��o�����ʂ̐F�����ׂĐԂł���m���� �ł���B
�ł���B
(3) 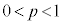 �Ƃ��A�e����Ŏ��o�����ʂ͔��ɖ߂��Ȃ����̂Ƃ���B3��̑���ŐԂ��ʂƔ����ʂ����傤��2�����o���m����
�Ƃ��A�e����Ŏ��o�����ʂ͔��ɖ߂��Ȃ����̂Ƃ���B3��̑���ŐԂ��ʂƔ����ʂ����傤��2�����o���m���� �ł���B
�ł���B �܂��A3��̑���Ŏ��o�����Ԃ��ʂƔ����ʂ̐����������m����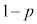 �ƂȂ�̂�
�ƂȂ�̂�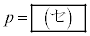 �̂Ƃ��ł���B
�̂Ƃ��ł���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�u2��̑���Ŏ��o�����ʂ̐F�����ׂĐԁv�Ƃ����\���ɑ����_���Ȃ��悤�ɁB2��ڂ̋ʂ̐F���ԁA�ƌ����Ă���̂ł͂Ȃ��A1��ڂ̋ʂ̐F�����ׂĐԂł����Ă���2��ڂ̋ʂ̐F�����ׂĐԁA�Ƃ������Ƃł��B
(1)(�R) �e����Ŏ��o�����ʂ����ɖ߂��̂ŁA1��ځA2��ڂœ������Ƃ��J��Ԃ���܂��B1��̑���ɂ����āA
�E�\���o���ꍇ(�m��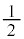 )�A���o���ꂽ1���Ԃł����m����
)�A���o���ꂽ1���Ԃł����m����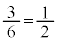 �@����@
�@����@ �E�����o���ꍇ(�m��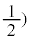 �A���o���ꂽ2���Ƃ��ɐԂł���m���́A�S���ۂ�6�̋ʂ���2���Ƃ�̂�
�A���o���ꂽ2���Ƃ��ɐԂł���m���́A�S���ۂ�6�̋ʂ���2���Ƃ�̂�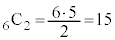 �ʂ�A2���Ƃ��ɐԂɂȂ�̂�3�̐ԋʂ���2���Ƃ�̂�
�ʂ�A2���Ƃ��ɐԂɂȂ�̂�3�̐ԋʂ���2���Ƃ�̂�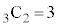 �ʂ�A����āA
�ʂ�A����āA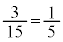 �@����A
�@����A 2�Ƃ��Ԃ̊m���́A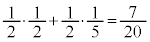 2��̑���Ŏ��o�����ʂ̐F�����ׂĐԂł����m���́A
2��̑���Ŏ��o�����ʂ̐F�����ׂĐԂł����m���́A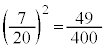 ......[��]
......[��]
(�T) 3��̑���Ŏ��o�����ʂ̌���5��(1�{2�{2��)�ɂȂ�̂́A3��̑���̂���2���A1�\�A�ƂȂ�Ƃ��ŁA3��̑���̂ǂ̉�ŕ\���o�邩��3�ʂ肠��A���̊m���́A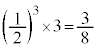
�Ⴆ�A1��ڂ��\��2��ڂ�3��ڂ����̏ꍇ�A�@�C�A���A���ׂĐԋʂɂȂ�m���́A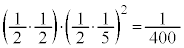 2��ڂ��\��1��ڂ�3��ڂ����̏ꍇ���A3��ڂ��\��1��ڂ�2��ڂ����̏ꍇ��������
2��ڂ��\��1��ڂ�3��ڂ����̏ꍇ���A3��ڂ��\��1��ڂ�2��ڂ����̏ꍇ��������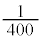 �ŁA3��̑���Ŏ��o�����ʂ����ׂĐԂƂȂ�m���́A
�ŁA3��̑���Ŏ��o�����ʂ����ׂĐԂƂȂ�m���́A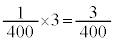 3��̑���Ŏ��o�����ʂ̑�����5�ł���Ƃ��������̉��ŁA���o�����ʂ̐F�����ׂĐԂł���m���́A
3��̑���Ŏ��o�����ʂ̑�����5�ł���Ƃ��������̉��ŁA���o�����ʂ̐F�����ׂĐԂł���m���́A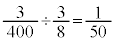 ......[��]�@(�����t���m�����Q��)
......[��]�@(�����t���m�����Q��)
(2)(�V) �e����Ŏ��o�����ʂ͔��ɖ߂��Ȃ��̂ŁA1��ڂ�2��ڂł͋ʂ̌��ɈႢ������܂��B
(i) 1��ڂ��\(�m��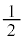 )�̂Ƃ��A���o�����1���Ԃ̊m���́A6����3�̐Ԃ̂�����1���Ƃ�(�m��
)�̂Ƃ��A���o�����1���Ԃ̊m���́A6����3�̐Ԃ̂�����1���Ƃ�(�m��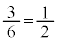 )�A
)�A �E2��ڂ��\(�m��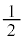 )�̂Ƃ��A���o�����1���Ԃ̊m���́A5����2�̐Ԃ̂�����1���Ƃ�m����
)�̂Ƃ��A���o�����1���Ԃ̊m���́A5����2�̐Ԃ̂�����1���Ƃ�m����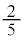
�E2��ڂ���(�m��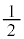 )�̂Ƃ��A���o�����2���Ƃ��ɐԂ̊m���́A5����2����āA2�Ƃ��Ԃ̊m����
)�̂Ƃ��A���o�����2���Ƃ��ɐԂ̊m���́A5����2����āA2�Ƃ��Ԃ̊m����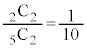
(ii) 1��ڂ���(�m��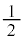 )�̂Ƃ��A6�̋ʂ���2���̂�
)�̂Ƃ��A6�̋ʂ���2���̂�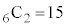 �ʂ�A3�̐Ԃ̂���2���Ƃ�̂�
�ʂ�A3�̐Ԃ̂���2���Ƃ�̂�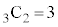 �ʂ�A���o�����2���Ƃ��ɐԂ̊m���́A
�ʂ�A���o�����2���Ƃ��ɐԂ̊m���́A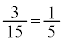
�E2��ڂ��\(�m��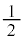 )�̂Ƃ��A���o�����1���Ԃ̊m���́A4�̋ʂ���1�̐Ԃ��Ƃ�m����
)�̂Ƃ��A���o�����1���Ԃ̊m���́A4�̋ʂ���1�̐Ԃ��Ƃ�m����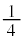
�E2��ڂ����̂Ƃ��A���o�����2���Ƃ��ɐ�(���Ƃ���Ɛԋʂ�4�ɂȂ��Ă��܂��܂�)�Ƃ������Ƃ͋N����܂���B
�ȏ���A2��̑���Ŏ��o�����ʂ̐F�����ׂĐԂł����m���́A 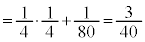 ......[��]
......[��]
 (3)(�X) 3��̑���ŐԋʂƔ��ʂ�2�����o���̂ŁA3��̑����4�̋ʂ����o�����ƂɂȂ�܂��B�܂�A3��̑���̂����A2�\(�m��p)�A1��(�m��
(3)(�X) 3��̑���ŐԋʂƔ��ʂ�2�����o���̂ŁA3��̑����4�̋ʂ����o�����ƂɂȂ�܂��B�܂�A3��̑���̂����A2�\(�m��p)�A1��(�m��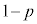 )�ł��B3��̂����ǂ̉�����3�ʂ肠��܂��B�Ⴆ�A�\�\���Əo���Ƃ��āA6�̋ʂ����o�����ɕ��ׂ�Ƃ��A6�̂����ǂ�3��ԋʂɂ��邩��
)�ł��B3��̂����ǂ̉�����3�ʂ肠��܂��B�Ⴆ�A�\�\���Əo���Ƃ��āA6�̋ʂ����o�����ɕ��ׂ�Ƃ��A6�̂����ǂ�3��ԋʂɂ��邩��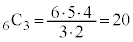 �ʂ肠���ē��l�Ɋm���炵���A���̂����A���o�����4�̒��łǂ�2��ԋʂɂ��邩��
�ʂ肠���ē��l�Ɋm���炵���A���̂����A���o�����4�̒��łǂ�2��ԋʂɂ��邩��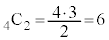 �ʂ�A���o�����4�ȊO��2�̂ǂ��炪�Ԃ���2�ʂ�(�E�}���Q��)�B�\���\�A���\�\�ł������ł��B
�ʂ�A���o�����4�ȊO��2�̂ǂ��炪�Ԃ���2�ʂ�(�E�}���Q��)�B�\���\�A���\�\�ł������ł��B����āA3��̑���ŐԂ��ʂƔ����ʂ����傤��2�����o���m���́A
�ʉ��D�Ⴆ�A�\�\���Əo��Ƃ��A�e��A��1�A��1�A��2�Ǝ��o���ꍇ�ƁA��1�A��1�A�Ԕ�1�����o���ꍇ(�����ł���ɁA�ԂƔ�������ւ�����ꍇ������)�Ƃ��l�����܂��B
1��ڂ�6�̋ʂ���3�̐ԋʂ̂�����1�����o���m����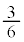 �C2��ڂ�5�̋ʂ���2�̐ԋʂ̂�����1�����o���m����
�C2��ڂ�5�̋ʂ���2�̐ԋʂ̂�����1�����o���m����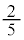 �C3��ڂ́A4�̋ʂ̂���2�����o���̂�
�C3��ڂ́A4�̋ʂ̂���2�����o���̂�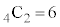 �ʂ�A���̂���3�̔��ʂ̂�����2�����o���̂�
�ʂ�A���̂���3�̔��ʂ̂�����2�����o���̂�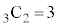 �ʂ�Ŋm����
�ʂ�Ŋm����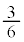 �C�\�\���Əo�Đ�1�A��1�A��2�Ǝ��o���m���́A
�C�\�\���Əo�Đ�1�A��1�A��2�Ǝ��o���m���́A �\�\���Əo�āA1��ڂɐԂ����o�����Ƃ��A2��ڂ�3�̔��ʂ̂�����1�����o���m����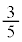 �C3��ڂ�2�̐ԋʂ̂�����1��2�̔��ʂ̂�����1�����o���m����
�C3��ڂ�2�̐ԋʂ̂�����1��2�̔��ʂ̂�����1�����o���m����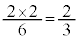 �C�\�\���Əo�Đ�1�A��1�A����1����2�Ǝ��o���m���́A
�C�\�\���Əo�Đ�1�A��1�A����1����2�Ǝ��o���m���́A ��L�ŐԂƔ�������ւ��ꍇ���܂߂āA�\�\���Əo�āA��2��2�����o���m���́A
�\���\�A���\�\�Əo��ꍇ�������m���ŁA���߂�m���́A
(�Z) 3��̑���ŁA3�ȏ�̋ʂ����o�����̂ŁA�Ԃ�����1�����o���A���邢�́A�Ԃ�����0�A�Ƃ������Ƃ͋N����܂���B3��̑���ŁA�Ԃ�����3�����o���Ƃ��́A3��Ƃ��u�����o��2���ʂ����o���v�̂ŁA6�S�����o���ĐԂ�����3���ɂȂ�܂��B���̊m����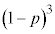 �ł��B(�X)���܂߂ĐԔ������ɂȂ�m���́A
�ł��B(�X)���܂߂ĐԔ������ɂȂ�m���́A ���ꂪ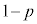 �ɓ������Ȃ�Ƃ��A
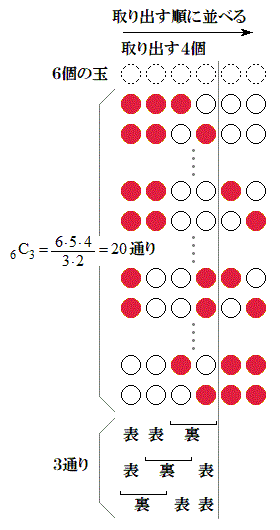
�ɓ������Ȃ�Ƃ��A 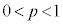 ���A
���A
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@�c�嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B