�c�嗝�H���w'20�N[2]
(1) 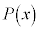 �𐮎��Ƃ��A
�𐮎��Ƃ��A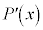 ��
��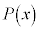 �̓����Ƃ���B���̂Ƃ��A
�̓����Ƃ���B���̂Ƃ��A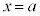 ��������
��������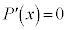 �̉��ƂȂ邱�Ƃ́A
�̉��ƂȂ邱�Ƃ́A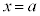 ��������
��������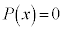 ��2�d���ƂȂ邽�߂̕K�v�����ł��邱�Ƃ��ؖ����Ȃ����B
��2�d���ƂȂ邽�߂̕K�v�����ł��邱�Ƃ��ؖ����Ȃ����B
(2) k��0�łȂ��������Ƃ��A������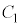 �F
�F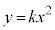 �Ɖ~
�Ɖ~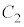 �F
�F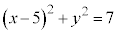 �̋��L�_�̌��͍ő��
�̋��L�_�̌��͍ő�� �ł���B
�ł���B
(3) (2)�ɂ����āA������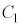 �Ɖ~
�Ɖ~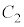 �̋��L�_�̌������傤��1�ƂȂ�k���l����B���̂Ƃ��A���L�_��x���W��k�̒l�ɂ�炸
�̋��L�_�̌������傤��1�ƂȂ�k���l����B���̂Ƃ��A���L�_��x���W��k�̒l�ɂ�炸 �ł���B�܂��Ak�̎�蓾��l��
�ł���B�܂��Ak�̎�蓾��l�� �ł���B
�ł���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�f���ɐi�߂��(3)�ōs���l�܂邩���m��܂���B(1)�����܂����p���邱�Ƃ��l���܂��B
(1) 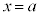 ��������
��������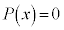 ��2�d���ł���A
��2�d���ł���A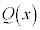 �𐮎��Ƃ��āA
�𐮎��Ƃ��āA �Ƃ����܂��B���̂Ƃ��A
����āA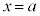 �͕�����
�͕�����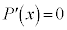 �̉��ł���A
�̉��ł���A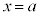 ��������
��������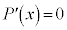 �̉��ƂȂ邱�Ƃ́A
�̉��ƂȂ邱�Ƃ́A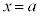 ��������
��������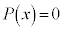 ��2�d���ƂȂ邽�߂��K�v�����ł��B(�ؖ��I)
��2�d���ƂȂ邽�߂��K�v�����ł��B(�ؖ��I)
�A������ƁA
�Ƃ����ƁA
�E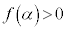 �̂Ƃ��A������
�̂Ƃ��A������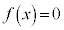 �͎��������������A
�͎��������������A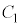 ��
��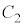 �̋��L�_�͂���܂���B
�̋��L�_�͂���܂���B �E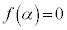 �̂Ƃ��A������
�̂Ƃ��A������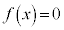 �͂���1�̎�����
�͂���1�̎�����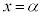 �������A
�������A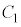 ��
��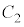 �̋��L�_��1�ł��B
�̋��L�_��1�ł��B �E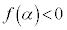 �̂Ƃ��A������
�̂Ƃ��A������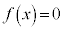 ��2�̎������������A
��2�̎������������A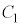 ��
��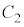 �̋��L�_��2�ł��B
�̋��L�_��2�ł��B �ȏ���A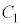 ��
��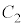 �̋��L�_�̌��͍ő��2�� ......[��]��[���Ř_�q�s�v�̌c�嗝�H�ł́A����I�ɂ́A
�̋��L�_�̌��͍ő��2�� ......[��]��[���Ř_�q�s�v�̌c�嗝�H�ł́A����I�ɂ́A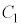 ��
��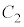 �̃O���t��`�����̌��ʂ͖��炩�ł��B
�̃O���t��`�����̌��ʂ͖��炩�ł��B
(3) (2)�ɂ����āA������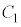 �Ɖ~
�Ɖ~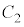 �̋��L�_�̌������傤��1�̂Ƃ��A(2)�ł̌������
�̋��L�_�̌������傤��1�̂Ƃ��A(2)�ł̌������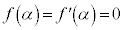 �ƂȂ�܂����A
�ƂȂ�܂����A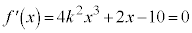 �̉�α�����߂��܂���B�����ŁA(1)�𗘗p���āAα���A������
�̉�α�����߂��܂���B�����ŁA(1)�𗘗p���āAα���A������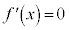 �ƕ�����
�ƕ�����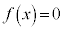 �����ʉ��ł��邱�Ƃ𗘗p���܂��B
�����ʉ��ł��邱�Ƃ𗘗p���܂��B 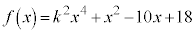 �@����@
�@����@
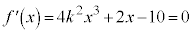 �@����A
�@����A���҂���ō����̍����������߂ɁA�@�~4�|�A�~x�����ƁA
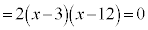 �@����B
�@����B�� 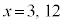
�@�C�A�����ʉ�α�́A�B�̉��ɂ��Ȃ�܂��B�A��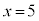 �Ƃ���ƁA
�Ƃ���ƁA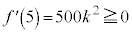 �ƂȂ�̂ŁA
�ƂȂ�̂ŁA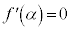 ���A
���A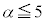 �ł���A���L�_��x���W�A�܂�A�@�C�A�̋��ʉ��́A
�ł���A���L�_��x���W�A�܂�A�@�C�A�̋��ʉ��́A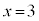 ......[��]���D���ʉ���
......[��]���D���ʉ���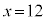 �̂Ƃ��A
�̂Ƃ��A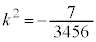 �ƂȂ�Ak�͎����ɂȂ�܂���B
�ƂȂ�Ak�͎����ɂȂ�܂���B
�A��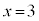 �Ƃ��āA
�Ƃ��āA �@�� 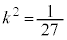 �C
�C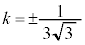 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@�c�嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B