���嗝�n���w'21�N�O��[4]
�ȉ��̖₢�ɓ�����B
(1) ���̊K�CL�Ɛ��̐���A�CB��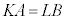 �����Ă���Ƃ���BK��4�Ŋ������]�肪L��4�Ŋ������]��Ɠ������Ȃ�AA��4�Ŋ������]���B��4�Ŋ������]��Ɠ��������Ƃ������B
�����Ă���Ƃ���BK��4�Ŋ������]�肪L��4�Ŋ������]��Ɠ������Ȃ�AA��4�Ŋ������]���B��4�Ŋ������]��Ɠ��������Ƃ������B (2) ���̐���a�Cb��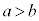 �����Ă���Ƃ���B���̂Ƃ��A
�����Ă���Ƃ���B���̂Ƃ��A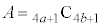 �C
�C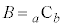 �ɑ���
�ɑ���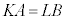 �ƂȂ�悤�Ȑ��̊K�CL�����݂��邱�Ƃ������B
�ƂȂ�悤�Ȑ��̊K�CL�����݂��邱�Ƃ������B (3) a�Cb��(2)�̒ʂ�Ƃ��A�����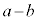 ��2�Ŋ�����Ƃ���B
��2�Ŋ�����Ƃ���B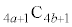 ��4�Ŋ������]���
��4�Ŋ������]���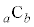 ��4�Ŋ������]��Ɠ��������Ƃ������B
��4�Ŋ������]��Ɠ��������Ƃ������B (4) 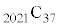 ��4�Ŋ������]������߂�B
��4�Ŋ������]������߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�r�s���ʼn���A�̗͂����̌������ł��B
(1) K�CL��4�Ŋ������]�肪�������̂ŁAm�𐮐��Ƃ��āA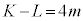 �Ƃ����܂��B���ӂ�A��������ƁA
�Ƃ����܂��B���ӂ�A��������ƁA 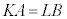 ���A
���A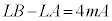 �C
�C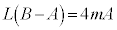
�E�ӂ�4�̔{���ł����AL�͊�Ȃ̂ŁA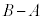 ��4�̔{���ł�(���������g���ď����ƁA
��4�̔{���ł�(���������g���ď����ƁA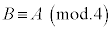 )�B�܂�AA��4�Ŋ������]���B��4�Ŋ������]��Ɠ������Ȃ�܂��B
)�B�܂�AA��4�Ŋ������]���B��4�Ŋ������]��Ɠ������Ȃ�܂��B (2) 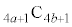 ��
��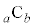 �����т���ȒP�ȊW�����v���������A���j�������Ȃ��̂ŁAa�Cb�ɊȒP�Ȑ��������邱�Ƃ���n�߂܂�(�g�ݍ��킹���Q��)�B
�����т���ȒP�ȊW�����v���������A���j�������Ȃ��̂ŁAa�Cb�ɊȒP�Ȑ��������邱�Ƃ���n�߂܂�(�g�ݍ��킹���Q��)�B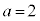 �C
�C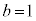 �Ƃ��Ă݂�ƁA
�Ƃ��Ă݂�ƁA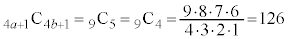 �C
�C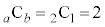 �C�Ŋm����
�C�Ŋm����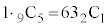 �ƂȂ�܂����A���������Ă��܂���B
�ƂȂ�܂����A���������Ă��܂���B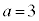 �C
�C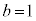 �Ƃ���ƁA
�Ƃ���ƁA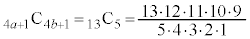 �C
�C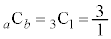 �C���q�E����ł����Z����Ă��鐔�ɉ�������ȁA�Ƃ����C�����܂����A�܂������܂���B
�C���q�E����ł����Z����Ă��鐔�ɉ�������ȁA�Ƃ����C�����܂����A�܂������܂���B a�Cb�������傫�����Ă݂܂��B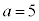 �C
�C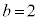 �Ƃ���ƁA
�Ƃ���ƁA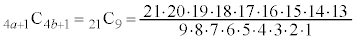 �C
�C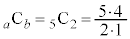 �C�����ő�ӂ���A
�C�����ő�ӂ���A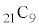 �̒���
�̒���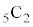 ���B��Ă��Ȃ����T���܂��B
���B��Ă��Ȃ����T���܂��B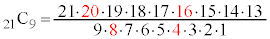 �̐Ԏ��̂Ƃ����
�̐Ԏ��̂Ƃ����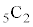 �ɕ��Ԑ�����4���������ĉB��Ă��܂��B����ŁA4�̔{������ɂ��Ă���̂��ȁA�Ƃ������ƂɋC�Â��܂��B
�ɕ��Ԑ�����4���������ĉB��Ă��܂��B����ŁA4�̔{������ɂ��Ă���̂��ȁA�Ƃ������ƂɋC�Â��܂��B �Ə����Ă݂�ƁA���q�ƕ��ꂪ�����Ƃ���ɂȂ��Ă���Ƃ���(����)�ƁA�����Ƃ������ɂȂ��Ă���Ƃ���(�Ԃ܂��̓s���N�F)�����邱�ƂɋC�Â��܂��B�悭����ƁA������A�����ĕ��ׂ�̂ŁA���R�̂��Ƃł����A�������Ƃ���A����������Ƃ��낪�݂��Ⴂ�ɕ��т܂��B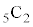 �ƂȂ�Ԏ��ȊO�̂Ƃ���ŋ����������Ă���Ƃ���(�s���N�F)���A
�ƂȂ�Ԏ��ȊO�̂Ƃ���ŋ����������Ă���Ƃ���(�s���N�F)���A 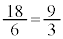 �C
�C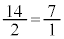
�ƂȂ��Ă��āA����A���ꕪ�q�Ƃ���ɂł��܂��B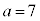 �C
�C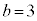 �ɂ��Ă݂܂��B
�ɂ��Ă݂܂��B 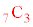 �ȊO�͕��q�E����Ɋ������сA����ŁA���̃J���N�����قڌ����Ă��܂��Ba�Cb�ɑ�����鐔�l��������x�傫�����Ȃ��ƌ����Ă��Ȃ����Ƃɒ��ӂ��K�v�ł��B
�ȊO�͕��q�E����Ɋ������сA����ŁA���̃J���N�����قڌ����Ă��܂��Ba�Cb�ɑ�����鐔�l��������x�傫�����Ȃ��ƌ����Ă��Ȃ����Ƃɒ��ӂ��K�v�ł��B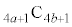 ����̓I�ɏ����ƁA���q�E�����4�̔{���ɂȂ�Ƃ����
����̓I�ɏ����ƁA���q�E�����4�̔{���ɂȂ�Ƃ����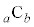 ���B��Ă��āA����ȊO�̕��ꕪ�q�Ƃ��ɋ����̂Ƃ���͖���ƕ��ꕪ�q�Ƃ��Ɋ�ɂł��āA����ȊO�͑S�ĕ��ꕪ�q�Ƃ��Ɋ�ł��B
���B��Ă��āA����ȊO�̕��ꕪ�q�Ƃ��ɋ����̂Ƃ���͖���ƕ��ꕪ�q�Ƃ��Ɋ�ɂł��āA����ȊO�͑S�ĕ��ꕪ�q�Ƃ��Ɋ�ł��B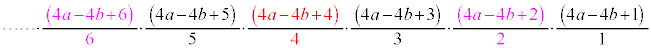 �@����@
�@����@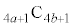 ����L�̇@�̂悤��
����L�̇@�̂悤��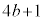 �̕����̐ς̌`�ɏ������Ƃ��A4���ƂɌ���镪�ꕪ�q�Ƃ���4�̔{���̂Ƃ����4�Ŗ��Ă������킹���
�̕����̐ς̌`�ɏ������Ƃ��A4���ƂɌ���镪�ꕪ�q�Ƃ���4�̔{���̂Ƃ����4�Ŗ��Ă������킹���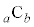 �ɂȂ�܂��B����ȊO�̕��ꕪ�q�Ƃ��ɋ����̂Ƃ���́A���ꕪ�q�Ƃ�4�Ŋ����2�]�鐔�ŁA2�Ŗ���ƁA���ꕪ�q�Ƃ��Ɋ�ɂȂ�܂��B�c��͍ŏ����番�ꕪ�q�Ƃ��Ɋ�ł��B
�ɂȂ�܂��B����ȊO�̕��ꕪ�q�Ƃ��ɋ����̂Ƃ���́A���ꕪ�q�Ƃ�4�Ŋ����2�]�鐔�ŁA2�Ŗ���ƁA���ꕪ�q�Ƃ��Ɋ�ɂȂ�܂��B�c��͍ŏ����番�ꕪ�q�Ƃ��Ɋ�ł��B
������A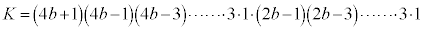 �@����B
�@����B
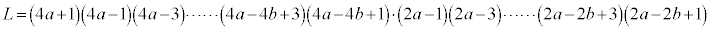 �@����C
�@����C�Ƃ���AK�CL�͐��̊�ŁA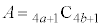 �C
�C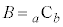 �ɑ���
�ɑ���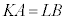 �ƂȂ�܂��B
�ƂȂ�܂��B (3) �@�̉E�ӂł������킳��Ă��镪���̕��ꕪ�q���Ƃ��Ɋ�̂Ƃ���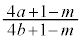 (
(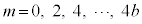 )�́A���q���番��������ƁA
)�́A���q���番��������ƁA ��4�̔{���Ȃ̂ŁA���q��4�Ŋ������]��ƕ����4�Ŋ������]��Ƃ͓������Ȃ�܂��B
�@�̉E�ӂŁA4�̔{���łȂ����������q�E����ɓ���Ƃ���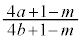 (
(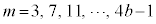 )�́A�A���ɂ����āA2�Ŗ���
)�́A�A���ɂ����āA2�Ŗ���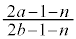 (
(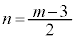 �C�܂�A
�C�܂�A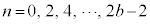 )�ƂȂ�܂����A���q���番��������ƁA
)�ƂȂ�܂����A���q���番��������ƁA �́A��蕶���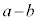 ��2�Ŋ�����̂ŁA4�̔{���ƂȂ�A���q��4�Ŋ������]��ƕ����4�Ŋ������]��͓������Ȃ�܂��B����āA�A���E�ӂ�
��2�Ŋ�����̂ŁA4�̔{���ƂȂ�A���q��4�Ŋ������]��ƕ����4�Ŋ������]��͓������Ȃ�܂��B����āA�A���E�ӂ�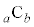 �ȊO�̂Ƃ���ł������킳��Ă���S�Ă̕����́A���ꕪ�q�Ƃ��Ɋ�ł����āA�������A����ƕ��q��4�Ŋ������]�肪�������Ȃ�܂��B
�ȊO�̂Ƃ���ł������킳��Ă���S�Ă̕����́A���ꕪ�q�Ƃ��Ɋ�ł����āA�������A����ƕ��q��4�Ŋ������]�肪�������Ȃ�܂��B
�]���āA�A���̕�����������킹���B��K�C�A���̕��q���������킹���C��L�ɂ��Ă��AK��L��4�Ŋ������]�肪�������Ȃ�܂��B(2)���A���̊K�CL��p���āA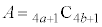 �C
�C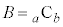 �ɑ���
�ɑ���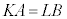 �ƂȂ�AK��L��4�Ŋ������]�肪�������Ȃ�̂ŁA(1)���A
�ƂȂ�AK��L��4�Ŋ������]�肪�������Ȃ�̂ŁA(1)���A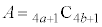 ��4�Ŋ������]��ƁA
��4�Ŋ������]��ƁA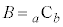 ��4�Ŋ������]��Ƃ͓������Ȃ�܂��B
��4�Ŋ������]��Ƃ͓������Ȃ�܂��B (4) 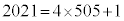 �C
�C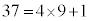 �Ȃ̂ŁA(3)���A
�Ȃ̂ŁA(3)���A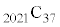 ��4�Ŋ������]���
��4�Ŋ������]���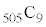 ��4�Ŋ������]��Ƃ͂Ƃ͓������Ȃ�܂��B
��4�Ŋ������]��Ƃ͂Ƃ͓������Ȃ�܂��B 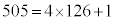 �C
�C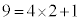 �Ȃ̂ŁA(3)���A
�Ȃ̂ŁA(3)���A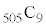 ��4�Ŋ������]���
��4�Ŋ������]���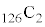 ��4�Ŋ������]��Ƃ͓������Ȃ�܂��B
��4�Ŋ������]��Ƃ͓������Ȃ�܂��B7875��4�Ŋ����3�]��̂ŁA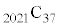 ��4�Ŋ������]���3 ......[��]
��4�Ŋ������]���3 ......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 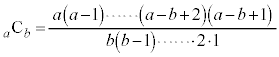
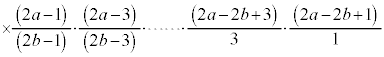 �@(
�@(