東京大学理系2021年前期数学入試問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
[1] a，bを実数とする。座標平面上の放物線
C：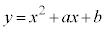
は放物線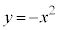
と2つの共有点を持ち、一方の共有点のx座標は
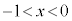を満たし、他方の共有点x座標は
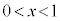を満たす。
(1) 点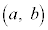
のとりうる範囲を座標平面上に図示せよ。 (2) 放物線Cの通りうる範囲を座標平面上に図示せよ。
[解答へ]
[2] 複素数a，b，cに対して整式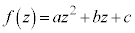
を考える。iを虚数単位とする。
(1) α，β，γを複素数とする。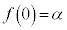
，
，
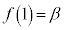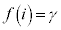が成り立つとき、a，b，cをそれぞれα，β，γで表せ。 (2) 
，
，
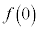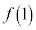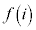がいずれも1以上2以下の実数であるとき、
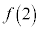のとりうる範囲を複素数平面上に図示せよ。
[解答へ]
[3] 関数
に対して、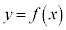
のグラフをCとする。点A
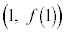におけるCの接線を
：
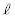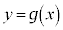
(1) Cと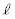
の共有点でAと異なるものがただ1つ存在することを示し、その点のx座標を求めよ。 (2) (1)で求めた共有点のx座標をαとする。定積分
を計算せよ。
[解答へ]
[4] 以下の問いに答えよ。
(1) 正の奇数K，Lと正の整数A，Bが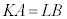
を満たしているとする。Kを4で割った余りがLを4で割った余りと等しいならば、Aを4で割った余りはBを4で割った余りと等しいことを示せ。 (2) 正の整数a，bが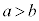
を満たしているとする。このとき、
，
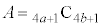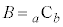に対して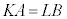
となるような正の奇数K，Lが存在することを示せ。 (3) a，bは(2)の通りとし、さらに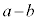
が2で割り切れるとする。
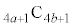を4で割った余りは
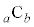を4で割った余りと等しいことを示せ。 (4) 
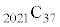を4で割った余りを求めよ。 [解答へ]
[5] aを正の実数とする。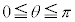
におけるθの関数
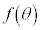を、座標平面上の2点A
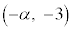，P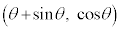
間の距離APの2乗として定める。
(1) 
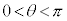の範囲に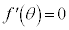
となるθがただ1つ存在することを示せ。 (2) 以下が成り立つようなαの範囲を求めよ。
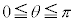におけるθの関数
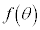は、区間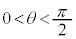
のある点において最大になる。
[6] 定数b，c，p，q，rに対し、
がxについての恒等式であるとする。
(1) 
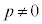であるとき、q，rをp，bで表せ。 (2) 
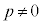とする。b，cが定数aを用いて 
，
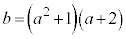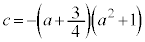
と表されているとき、有理数を係数とするt についての整式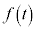
と
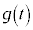で を満たすものを1組求めよ。
(3) aを整数とする。xの4次式
が有理数を係数とする2次式の積に因数分解できるようなaをすべて求めよ。
[解答へ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
東大理系数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
