���H�啨��'20�N�O��[2]
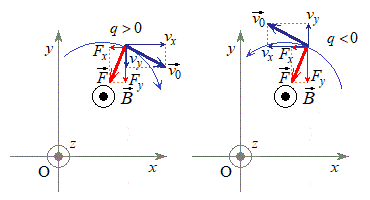
 �d���ꒆ�ɂ����鎿��m�C�d��q�̉דd���q�̉^�����l�@����B�f��̂Ȃ�����Aq�͐���������̒l����肤����̂Ƃ���B�������x
�d���ꒆ�ɂ����鎿��m�C�d��q�̉דd���q�̉^�����l�@����B�f��̂Ȃ�����Aq�͐���������̒l����肤����̂Ƃ���B�������x �́A���ԓI�ɕω����邱�Ƃ͂Ȃ��Ƃ���B�܂��A�������x
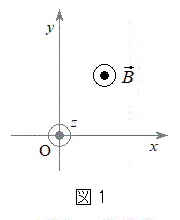
�́A���ԓI�ɕω����邱�Ƃ͂Ȃ��Ƃ���B�܂��A�������x �̌����́A�}1�̂悤�Ɏ��ʂ̗�����\�̌����ł���A���̌�����z���̐��̌����Ƃ��A�דd���q��xy���ʓ����^��������̂Ƃ���B�Ȃ��A�דd���q�͐^���^��������̂Ƃ��A�܂��A�d�͂̉e���͖����ł�����̂Ƃ���B
�̌����́A�}1�̂悤�Ɏ��ʂ̗�����\�̌����ł���A���̌�����z���̐��̌����Ƃ��A�דd���q��xy���ʓ����^��������̂Ƃ���B�Ȃ��A�דd���q�͐^���^��������̂Ƃ��A�܂��A�d�͂̉e���͖����ł�����̂Ƃ���B
[A]�@�������x�̑傫�� �̈�l�Ȏ��ꒆ�ŁA�דd���q������
�̈�l�Ȏ��ꒆ�ŁA�דd���q������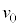 ��xy���ʏ�̓����~�^�����s���Ă���Ƃ���B�Ȃ��A�ݖ�[A]�ł́A�d��͂������Ă��Ȃ����̂Ƃ���B�ȉ��̖�ɓ�����B
��xy���ʏ�̓����~�^�����s���Ă���Ƃ���B�Ȃ��A�ݖ�[A]�ł́A�d��͂������Ă��Ȃ����̂Ƃ���B�ȉ��̖�ɓ�����B
(a) �~�^���̔��a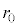 ���Am�C
���Am�C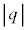 �C
�C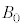 �C
�C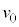 �̂����K�v�Ȃ��̂�p���ĕ\���B
�̂����K�v�Ȃ��̂�p���ĕ\���B
(b) �דd���q�̑��x��x�Cy���������ꂼ��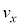 �C
�C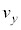 �Ƃ��A�דd���q����͂�x�Cy���������ꂼ��
�Ƃ��A�דd���q����͂�x�Cy���������ꂼ��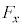 �C
�C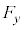 �Ƃ���B
�Ƃ���B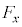 �����
�����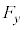 ���Aq�C
���Aq�C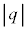 �C
�C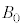 �C
�C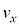 �C
�C �̂����K�v�Ȃ��̂�p���Ă��ꂼ��\���B
�̂����K�v�Ȃ��̂�p���Ă��ꂼ��\���B
[B]�@���ɁA�������x�̌�����z���̐��̌����̂܂܁A �ł͎������x�̑傫����
�ł͎������x�̑傫����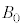 �C
�C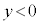 �ł͎������x�̑傫����
�ł͎������x�̑傫����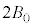 �ł���Ƃ���B�Ȃ��A�ݖ�[B]�ł��A�d��͂������Ă��Ȃ����̂Ƃ���B
�ł���Ƃ���B�Ȃ��A�ݖ�[B]�ł��A�d��͂������Ă��Ȃ����̂Ƃ���B ����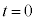 �ɂ����āA�דd���q�����_O��y���̐��̌����ɑ���
�ɂ����āA�דd���q�����_O��y���̐��̌����ɑ���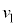 �Œʉ߂����Bn�𐳂̐����Ƃ��āA�דd���q��
�Œʉ߂����Bn�𐳂̐����Ƃ��āA�דd���q��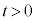 ��n��ڂ�x�������鎞��(���Ȃ킿y���W���[���ƂȂ鎞��)��
��n��ڂ�x�������鎞��(���Ȃ킿y���W���[���ƂȂ鎞��)��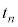 �C���̂Ƃ���x���W��
�C���̂Ƃ���x���W��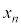 �Ə������Ƃɂ���B�ȉ��̖�ɓ�����B
�Ə������Ƃɂ���B�ȉ��̖�ɓ�����B
(c) m�Cq�C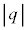 �C
�C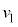 �C
�C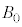 �̂����K�v�Ȃ��̂�p���āA
�̂����K�v�Ȃ��̂�p���āA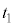 �C
�C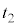 �C
�C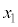 �����
����� ��\���B
��\���B
 (d) �דd���q��y���W�̂Ƃ肤��ő�l����эŏ��l���Am�C
(d) �דd���q��y���W�̂Ƃ肤��ő�l����эŏ��l���Am�C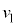 �Cq�C
�Cq�C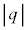 �C
�C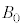 �̂����K�v�Ȃ��̂�p���ĕ\���B����ɁA���̃O���t�ɁA
�̂����K�v�Ȃ��̂�p���ĕ\���B����ɁA���̃O���t�ɁA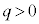 �̏ꍇ��
�̏ꍇ��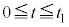 �̊Ԃ̉דd���q�̋O��(���~)���L����Ă���B����ɂЂ��Â��A
�̊Ԃ̉דd���q�̋O��(���~)���L����Ă���B����ɂЂ��Â��A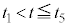 �̊Ԃ̉דd���q�̋O�Ղ̊T�`�����̃O���t�ɕ`��������B
�̊Ԃ̉דd���q�̋O�Ղ̊T�`�����̃O���t�ɕ`��������B
 [C]�@���ɁAz���̐��̌����̎���ɉ����āA�d�������ꍇ���l����B�ݖ�[C]�ł́A�������x�͈�l�ő傫��
[C]�@���ɁAz���̐��̌����̎���ɉ����āA�d�������ꍇ���l����B�ݖ�[C]�ł́A�������x�͈�l�ő傫�� �Ƃ���B�����A�d���y���̐��̌����������Ă���A��l�ő傫��
�Ƃ���B�����A�d���y���̐��̌����������Ă���A��l�ő傫�� �Ƃ���B����
�Ƃ���B���� �ɂ����āA�דd���q�͌��_O�ɐÎ~���Ă���Ƃ���B�����ŁA����t�ɂ�����דd���q�̑��x��x�Cy�������A���ꂼ��
�ɂ����āA�דd���q�͌��_O�ɐÎ~���Ă���Ƃ���B�����ŁA����t�ɂ�����דd���q�̑��x��x�Cy�������A���ꂼ��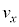 �C
�C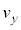 �ƕ\�����ƂƂ���B�ȉ��̖�ɓ�����B
�ƕ\�����ƂƂ���B�ȉ��̖�ɓ�����B
(e) ����t�ɂ����āA�דd���q����͂�x�Cy���������ꂼ��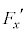 �C
�C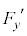 �Ƃ���B
�Ƃ���B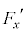 �����
�����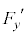 ���Aq�C
���Aq�C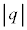 �C
�C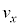 �C
�C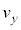 �C
�C �C
�C �̂����K�v�Ȃ��̂�p���Ă��ꂼ��\���B
�̂����K�v�Ȃ��̂�p���Ă��ꂼ��\���B
(f) ���鑬��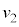 ��x���̐��̌����ɓ����x�^������ϑ��҂��猩���ꍇ�ɂ́A�דd���q�̉^���������~�^���Ɍ�����B m�Cq�C
��x���̐��̌����ɓ����x�^������ϑ��҂��猩���ꍇ�ɂ́A�דd���q�̉^���������~�^���Ɍ�����B m�Cq�C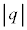 �C
�C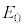 �����
����� �̂����K�v�Ȃ��̂�p����
�̂����K�v�Ȃ��̂�p����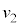 ��\���B
��\���B
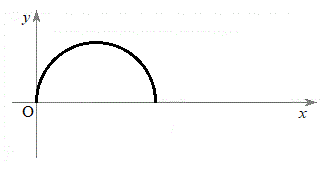
(g) 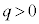 �̏ꍇ��
�̏ꍇ��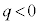 �̏ꍇ�̂��ꂼ��ɂ��A����
�̏ꍇ�̂��ꂼ��ɂ��A����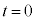 ���炵�炭�̊Ԃ́A�Î~�����ϑ��҂��猩���דd���q�̋O�Ղ̊T�`�Ƃ��āA�����Ƃ��ӂ��킵�����̂��A�}2�̑I�����@�`�I���炻�ꂼ��1���I�ׁB
���炵�炭�̊Ԃ́A�Î~�����ϑ��҂��猩���דd���q�̋O�Ղ̊T�`�Ƃ��āA�����Ƃ��ӂ��킵�����̂��A�}2�̑I�����@�`�I���炻�ꂼ��1���I�ׁB
(h) 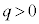 �̏ꍇ���l����B�דd���q��y���W�̂Ƃ肤��ő�l
�̏ꍇ���l����B�דd���q��y���W�̂Ƃ肤��ő�l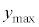 �́A(f)�ŋ��߂�
�́A(f)�ŋ��߂� ��p���ĉ��L�̂悤�ɂȂ�B��
��p���ĉ��L�̂悤�ɂȂ�B�� �ɓ��Ă͂܂鐔����m�Cq�C
�ɓ��Ă͂܂鐔����m�Cq�C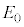 �C
�C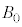 �̂����K�v�Ȃ��̂�p���ĕ\���B
�̂����K�v�Ȃ��̂�p���ĕ\���B
�܂��A�Î~�����ϑ��҂��猩���ꍇ�ɁA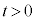 �ɂ����čŏ���
�ɂ����čŏ���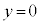 �ƂȂ�Ƃ���x���W�̐�Βl
�ƂȂ�Ƃ���x���W�̐�Βl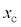 �́A���L�̂悤��
�́A���L�̂悤��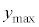 �̒萔�{�ƂȂ��Ă���B��
�̒萔�{�ƂȂ��Ă���B�� �߂�B
�߂�B
 (i) ��������
(i) ��������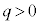 �̏ꍇ���l����B�Î~�����ϑ��҂��猩���ꍇ�ɁA����
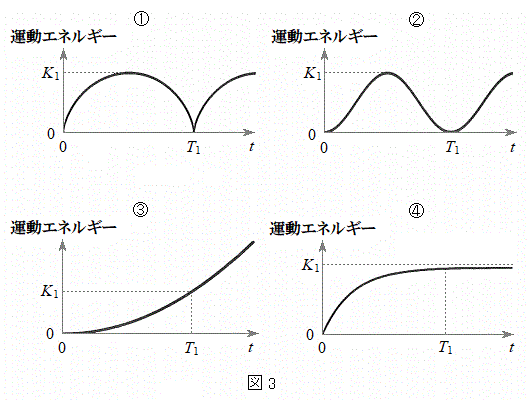
�̏ꍇ���l����B�Î~�����ϑ��҂��猩���ꍇ�ɁA����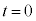 ���炵�炭�̊Ԃ̉דd���q�̉^���G�l���M�[�̕ω��̗l�q�Ƃ��Ă����Ƃ��ӂ��킵�����̂��A�}3�̑I�����@�`�C����I�ׁB�������A�}3�̉����ɂ���
���炵�炭�̊Ԃ̉דd���q�̉^���G�l���M�[�̕ω��̗l�q�Ƃ��Ă����Ƃ��ӂ��킵�����̂��A�}3�̑I�����@�`�C����I�ׁB�������A�}3�̉����ɂ���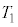 �́A�דd���q��y���W��
�́A�דd���q��y���W��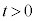 �ōŏ��Ƀ[���ƂȂ鎞����\���B
�ōŏ��Ƀ[���ƂȂ鎞����\���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@���ΐ����_���\�z�����A�C���V���^�C���́A���Z�œd���C�w���w�Ƃ��A�u���ꒆ�����鑬�x�ňړ�����d�ׂ͎��ꂩ��͂���v�A�ƏK���āA���̓d�ׂƓ������x�ňړ�����ϑ��҂��猩����A�d�ׂ͎~�܂��Č�����(���x�[��)�̂ɁA���̗͂͂ǂ��Ȃ��Ă��܂��̂��낤���A�ƁA�^��Ɏv�����A�Ƃ�����b���A�{�����ǂ����킩��܂��`�����Ă��܂��B
�قȂ���W�n�Ō�����A�����w�͂ǂ̂悤�ɂȂ�̂��A�Ƃ����^�₪���ΐ����_�̏o���_�ɂȂ��Ă���̂ł����A�{��ł��A�����x�^������ϑ��҂��玥�ꒆ�œ����~�^���Ɍ�����^���́A�Î~�����ϑ��҂��猩��Ƃǂ̂悤�ȉ^�����A�Ƃ������Ƃ��e�[�}�ɂȂ��Ă��܂��B
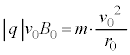 �@��
�@�� 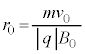 ......[��]�@���(1��)
......[��]�@���(1��)
 (b) �����~�^�����Ă���דd���q�̑��x
(b) �����~�^�����Ă���דd���q�̑��x �Ɨ�
�Ɨ� �̊W�͉E�}�̂悤�ɂȂ��Ă��܂�(�t���~���O����̖@�����Q��)�B
�̊W�͉E�}�̂悤�ɂȂ��Ă��܂�(�t���~���O����̖@�����Q��)�B �ł��B�O�p�`�̑������A
�ł��B�O�p�`�̑������A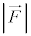 �F
�F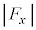 �F
�F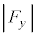 ��
��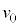 �F
�F �F
�F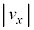 �C����āA
�C����āA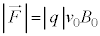 ���A
���A�܂��A�E�}�̏ŁA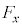 ��
�� �C
�C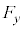 ��
��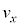 �̕������l����ƁA
�̕������l����ƁA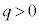 �̏ꍇ�́A
�̏ꍇ�́A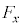 ��
��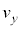 �͓������ŁA
�͓������ŁA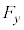 ��
��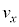 �͈ٕ����A
�͈ٕ����A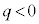 �̏ꍇ�́A
�̏ꍇ�́A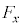 ��
��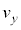 �͈ٕ���(�]���āA
�͈ٕ���(�]���āA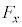 ��
��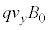 �͓�����)�ŁA
�͓�����)�ŁA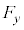 ��
��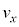 �͓�����(�]���āA
�͓�����(�]���āA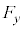 ��
��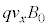 �͈ٕ���)�A����āA
�͈ٕ���)�A����āA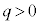 �C
�C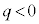 ������̏ꍇ���A
������̏ꍇ���A 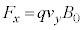 �C
�C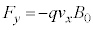 ......[��]
......[��]���D���ȏ��I�ɂ́A���x�Ɨ͂𐬕��ɕ����čl����Ήł��܂��B
[B](c) [B]��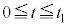 �̊Ԃ̓����~�^���̑�����
�̊Ԃ̓����~�^���̑�����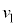 �C[A](a)�Ɠ��l�ɉ~�^���̔��a��
�C[A](a)�Ɠ��l�ɉ~�^���̔��a��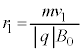 �@���(1��)�@�ł��B
�@���(1��)�@�ł��B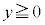 �̕����̓����~�^���̎���T�́A
�̕����̓����~�^���̎���T�́A
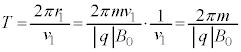 �@���(2��)
�@���(2��)���̊Ԃ̉~�^���͔�������(�O�Ղ͔��~)�ŁA
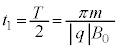 ......[��]
......[��]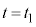 ��x��������ۂ̉דd���q�̑�����
��x��������ۂ̉דd���q�̑�����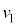 �ŁA
�ŁA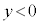 �ł͎������x�̑傫����
�ł͎������x�̑傫����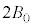 �Ȃ̂ŁA
�Ȃ̂ŁA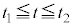 �ɂ����铙���~�^����(2��)��(1��)��
�ɂ����铙���~�^����(2��)��(1��)��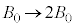 �Ƃ��Ď�����(2��)��
�Ƃ��Ď�����(2��)�� �C���a��(1��)��
�C���a��(1��)��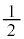 �C
�C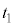 ��
��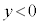 �̓����~�^���̔��������������āA
�̓����~�^���̔��������������āA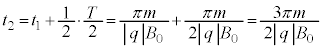 ......[��]
......[��]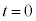 �Ɍ��_O��ʉ߂���Ƃ��A
�Ɍ��_O��ʉ߂���Ƃ��A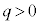 �̏ꍇ�́A�����I�ɓd����y���������ɗ���A�t���~���O����̖@�����x���������ɗ͂���
�̏ꍇ�́A�����I�ɓd����y���������ɗ���A�t���~���O����̖@�����x���������ɗ͂���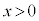 �̑��ɓ����~�^�����n�߁A
�̑��ɓ����~�^�����n�߁A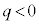 �̏ꍇ�́A�����I�ɓd����y���������ɗ���Ax���������ɗ͂���
�̏ꍇ�́A�����I�ɓd����y���������ɗ���Ax���������ɗ͂���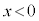 �̑��ɓ����~�^�����n�߂܂��B�]���āA�דd���q�̉^���͈͂́A
�̑��ɓ����~�^�����n�߂܂��B�]���āA�דd���q�̉^���͈͂́A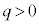 �ł�
�ł�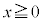 �C
�C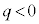 �ł�
�ł�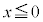 �ł��B
�ł��B
 �͔��a
�͔��a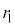 �̉~�^���̒��a
�̉~�^���̒��a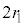 �ɓ������A
�ɓ������A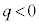 �̏ꍇ�ɒ��ӂ��āA(1��)���A
�̏ꍇ�ɒ��ӂ��āA(1��)���A ......[��]�@���(3��)
......[��]�@���(3��)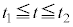 �ɂ����铙���~�^���̔��a��(1��)��
�ɂ����铙���~�^���̔��a��(1��)��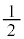 �Œ��a��
�Œ��a��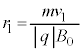 �C
�C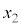 ��
��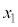 ���猴�_������
���猴�_������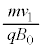 �����߂����Ƃ���(
�����߂����Ƃ���(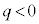 �̏ꍇ�ɒ���)�ŁA(3��)���A
�̏ꍇ�ɒ���)�ŁA(3��)���A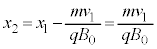 ......[��]
......[��]
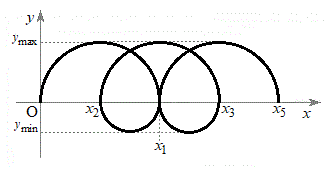 (d) y���W�̍ő�l
(d) y���W�̍ő�l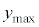 ��
��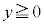 �̕����̓����~�^���̔��a�ɓ������A(1��)���A
�̕����̓����~�^���̔��a�ɓ������A(1��)���A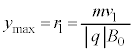 ......[��]
......[��]y���W�̍ŏ��l ��
��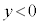 �̕����̓����~�^���̔��a�Ƀ}�C�i�X���������̂ŁA
�̕����̓����~�^���̔��a�Ƀ}�C�i�X���������̂ŁA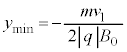 ......[��]
......[��]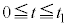 �̋O�Ղɑ�����
�̋O�Ղɑ�����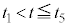 �̉דd���q�̋O�Ղ�`���ƁA���̊T�`�͉E�}�B
�̉דd���q�̋O�Ղ�`���ƁA���̊T�`�͉E�}�B
[C](e) (b)�ŋ��߂��͂ɁA�d��ɂ��y�������̗�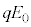 �������āA
�������āA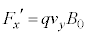 �C
�C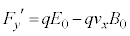 ......[��]
......[��]
(f) ���� ��x���̐��̌����ɓ����x�^������ϑ��҂��猩���דd���q�̑��Α��x��x������
��x���̐��̌����ɓ����x�^������ϑ��҂��猩���דd���q�̑��Α��x��x������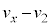 �ł��B(e)�̌��ʂŁA
�ł��B(e)�̌��ʂŁA 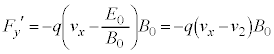 �@���(4��)
�@���(4��)�ƌ���ƁA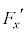 �C
�C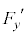 �́A(b)�̓����~�^������דd���q�����
�́A(b)�̓����~�^������דd���q����� �C
�C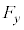 �̌��ʂ�
�̌��ʂ�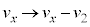 �Ƃ������̂ɂȂ�܂��B����āA�����x�^������ϑ��҂��猩���דd���q�̉^���������~�^���ƂȂ�(4��)���������邽�߂ɂ́A
�Ƃ������̂ɂȂ�܂��B����āA�����x�^������ϑ��҂��猩���דd���q�̉^���������~�^���ƂȂ�(4��)���������邽�߂ɂ́A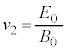 ......[��]���̌��ʂ́A����
......[��]���̌��ʂ́A����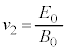 �œ����x�^������ϑ��҂��猩��ƁA�d��
�œ����x�^������ϑ��҂��猩��ƁA�d��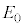 ���������Ȃ��Ȃ�(�t�����œ����傫�����U���d�����������A�d��
���������Ȃ��Ȃ�(�t�����œ����傫�����U���d�����������A�d��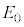 ��ł������܂�)�A[A]�Ɠ����ɂȂ�A�Ƃ������Ƃ��Ӗ����Ă��܂��B
��ł������܂�)�A[A]�Ɠ����ɂȂ�A�Ƃ������Ƃ��Ӗ����Ă��܂��B
����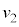 ��x���������ɉ^������ϑ��҂��猩�āA�d�ꂪ�����Ă���̂ŁA�דd���q��
��x���������ɉ^������ϑ��҂��猩�āA�d�ꂪ�����Ă���̂ŁA�דd���q��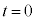 �Ɍ��_O�ŐÎ~���Ă����Ƃ��납��x���������ɑ���
�Ɍ��_O�ŐÎ~���Ă����Ƃ��납��x���������ɑ���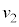 �œ����o��(�]���āA�����~�^������דd���q�̑�����
�œ����o��(�]���āA�����~�^������דd���q�̑�����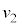 �ł�)�悤�Ɍ����܂��B�����I�ɓd�����A
�ł�)�悤�Ɍ����܂��B�����I�ɓd�����A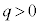 �̏ꍇ��x���������ɁA
�̏ꍇ��x���������ɁA �̏ꍇ��x���������ɗ���āA
�̏ꍇ��x���������ɗ���āA �̏ꍇ�́A�����o��������t���~���O����̖@�����Ay���������Ɏ��ꂩ��͂��ē����~�^�����J�n���A
�̏ꍇ�́A�����o��������t���~���O����̖@�����Ay���������Ɏ��ꂩ��͂��ē����~�^�����J�n���A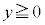 �͈̔͂œ����~�^������悤�Ɍ����܂��B
�͈̔͂œ����~�^������悤�Ɍ����܂��B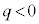 �̏ꍇ�́A�����o��������Ay���������Ɏ��ꂩ��͂��ē����~�^�����J�n���A
�̏ꍇ�́A�����o��������Ay���������Ɏ��ꂩ��͂��ē����~�^�����J�n���A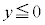 �͈̔͂œ����~�^������悤�Ɍ����܂��B
�͈̔͂œ����~�^������悤�Ɍ����܂��B
(g) �Î~�����ϑ��҂��猩��ƁAy�������̓d��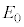 ������̂ŁA�דd���q�͗�
������̂ŁA�דd���q�͗�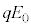 ���āA
���āA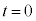 ����A
����A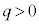 �Ȃ�y����������
�Ȃ�y����������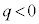 �Ȃ�y���������ɓ����n�߂܂��B�����o���ƁA�����I�ɓd���������̂Ŏ��ꂩ��͂��܂��B�����o��������A
�Ȃ�y���������ɓ����n�߂܂��B�����o���ƁA�����I�ɓd���������̂Ŏ��ꂩ��͂��܂��B�����o��������A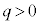 �̏ꍇ�́A�d����y���������ŁA�t���~���O����̖@�����Ax���������ɗ͂��܂��B
�̏ꍇ�́A�d����y���������ŁA�t���~���O����̖@�����Ax���������ɗ͂��܂��B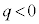 �̏ꍇ�́A��͂�d����y��������(�דd���q�������n�߂������q�̐����ŋt�����ɂȂ�܂����A�d�ׂ̐������قȂ�̂ŁA�d���̌����͂ǂ����y��������)�ŁAx���������ɗ͂��܂��B�ǂ���̏ꍇ���דd���q�́A
�̏ꍇ�́A��͂�d����y��������(�דd���q�������n�߂������q�̐����ŋt�����ɂȂ�܂����A�d�ׂ̐������قȂ�̂ŁA�d���̌����͂ǂ����y��������)�ŁAx���������ɗ͂��܂��B�ǂ���̏ꍇ���דd���q�́A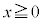 �͈̔͂ʼn^�����邱�ƂɂȂ�܂��B(f)�Ō��������悤�ɁA�דd���q��
�͈̔͂ʼn^�����邱�ƂɂȂ�܂��B(f)�Ō��������悤�ɁA�דd���q��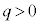 �̏ꍇ��
�̏ꍇ��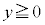 �͈̔́A
�͈̔́A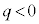 �̏ꍇ��
�̏ꍇ��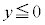 �͈̔͂ʼn^������(y�����́A�ϑ��҂�x�������̉^���̉e�����܂���)�̂ŁA
�͈̔͂ʼn^������(y�����́A�ϑ��҂�x�������̉^���̉e�����܂���)�̂ŁA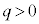 �̏ꍇ�̋O�Ղ͇@ ......[��]�@
�̏ꍇ�̋O�Ղ͇@ ......[��]�@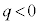 �̏ꍇ�̋O�Ղ͇B ......[��]
�̏ꍇ�̋O�Ղ͇B ......[��]
(h) (f)�ł̌����Ɋ�Â��čl���܂��B
(�A) ����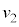 �œ����x�^������ϑ��҂��猩�āA
�œ����x�^������ϑ��҂��猩�āA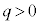 �̏ꍇ�A������
�̏ꍇ�A������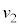 �̓����~�^���̔��a��[A](a)�Ɠ��l��
�̓����~�^���̔��a��[A](a)�Ɠ��l��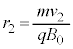 �C
�C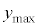 �͂��̉~�^���̒��a�ɓ�����(�����~�^���͈̔͂�
�͂��̉~�^���̒��a�ɓ�����(�����~�^���͈̔͂� )�A
)�A 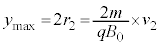 �@
�@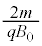 ......[��]
......[��]
(�C) ���_O���o�������דd���q��x����ɖ߂��Ă���܂łɓ����~�^��1�������̎���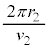 ��������܂��B����
��������܂��B����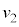 �ňړ����Ă���ϑ��҂ɂ͓����~�^�����Ă���悤�Ɍ�����̂ŁA���̊ϑ��҂ɂ͂��̊ԂɌ��_O����o�Č��_O�ɖ߂��Ă���悤�Ɍ����܂����A�Î~�����ϑ��҂ɂ́Ax�����ɑ���
�ňړ����Ă���ϑ��҂ɂ͓����~�^�����Ă���悤�Ɍ�����̂ŁA���̊ϑ��҂ɂ͂��̊ԂɌ��_O����o�Č��_O�ɖ߂��Ă���悤�Ɍ����܂����A�Î~�����ϑ��҂ɂ́Ax�����ɑ���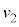 �ňړ�����ϑ��҂̈ړ�����
�ňړ�����ϑ��҂̈ړ�����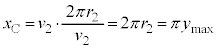 ���������悤�Ɍ����܂��B�@π ......[��]
���������悤�Ɍ����܂��B�@π ......[��]
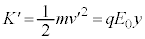 �@���(5��)
�@���(5��)�^������ϑ��҂��猩�Ă��A�Î~���Ă���ϑ��҂��猩�Ă��A�����x�^������דd���q��y�����̉^���� �͈̔͂œ����P�U���ŁA
�͈̔͂œ����P�U���ŁA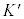 ��(5��)�����悤��y�Ɉˑ����ĕω������Ă���̂́A�A ......[��]�^���G�l���M�[���ő�ɂȂ�̂́A�}2�@��y���W���ő�ƂȂ�_�ɂ����Ăł��B(5��)�ɂ����āA
��(5��)�����悤��y�Ɉˑ����ĕω������Ă���̂́A�A ......[��]�^���G�l���M�[���ő�ɂȂ�̂́A�}2�@��y���W���ő�ƂȂ�_�ɂ����Ăł��B(5��)�ɂ����āA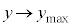 �Ƃ��āA���̓_�ł̉^���G�l���M�[
�Ƃ��āA���̓_�ł̉^���G�l���M�[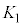 �́A
�́A 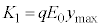 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���H�啨��TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 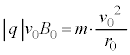 �@��
�@�� 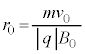 ......[��]�@���(1��)
......[��]�@���(1��)

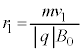 �@���(1��)�@�ł��B
�@���(1��)�@�ł��B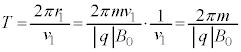 �@���(2��)
�@���(2��)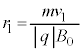 �C
�C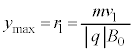 ......[��]
......[��]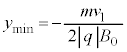 ......[��]
......[��]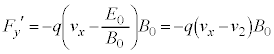 �@���(4��)
�@���(4��)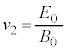 ......[��]
......[��]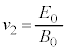 �œ����x�^������ϑ��҂��猩��ƁA�d��
�œ����x�^������ϑ��҂��猩��ƁA�d��