微分法の不等式への応用(2)の続き
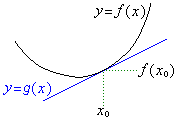右図のように例えば、下に凸な曲線
上の1点で接線
が引かれているとき、接点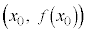
以外の点では全て、曲線は接線の上側に来ます。
従って、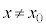
であれば、
です。
例4．n個の正数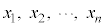
について、相加平均・相乗平均の不等式：
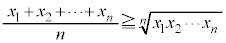を証明する。
[証明]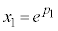 
，
，･･･，
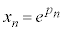となるような、
を考えます。
は、
より下に凸な関数です。
従って、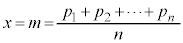
における接線は、接点
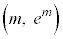を除いて、曲線
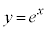の下側に来ます。
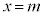における、
の接線は、
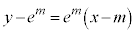より、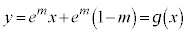
これより、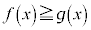
です。
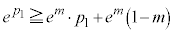
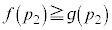より、
より、
･･････
より、
以上を辺々加えると、
(∵ 
)
∴ 
∴ 
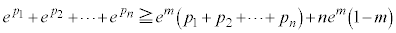
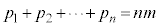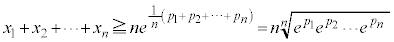
(証明終)
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 