�����@�̕s�����ւ̉��p(2)�@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
(1) �����𗘗p�����s�����̏ؖ�(�����@�̕s�����ւ̉��p���Q�Ƃ��Ă�������)
��1�D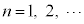 �ɑ��A
�ɑ��A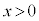 �ɂ����āA
�ɂ����āA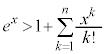
[�ؖ�]�@���w�I�A�[�@�ŏؖ����܂��B
�E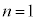 �̂Ƃ��A
�̂Ƃ��A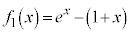 �Ƃ��āA
�Ƃ��āA
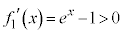 (
(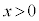 )���A
)���A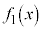 �͒P�������ŁA
�͒P�������ŁA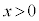 �ɂ����āA
�ɂ����āA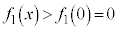
�� 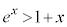
����āA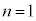 �̂Ƃ��^�s���������藧���܂��B�@���(�T)
�̂Ƃ��^�s���������藧���܂��B�@���(�T)
�E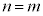 �̂Ƃ��^�s���������藧�Ɖ��肵�܂��B
�̂Ƃ��^�s���������藧�Ɖ��肵�܂��B
�܂�A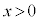 �ɂ����āA
�ɂ����āA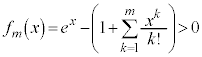 �����藧�Ɖ��肵�܂��B
�����藧�Ɖ��肵�܂��B
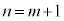 �̂Ƃ��A
�̂Ƃ��A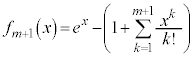 ���������ƁA
���������ƁA
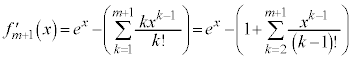
�����ŁA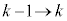 �Ɣԍ���t���ւ���ƁA
�Ɣԍ���t���ւ���ƁA
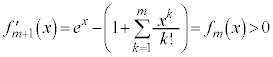 (
(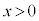 )���A
)���A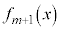 �͒P�������ŁA
�͒P�������ŁA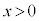 �ɂ����āA
�ɂ����āA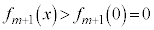
�� 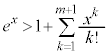
����āA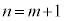 �̂Ƃ����^�s�����͐��藧���܂��B�@���(�U)
�̂Ƃ����^�s�����͐��藧���܂��B�@���(�U)
(�T)�C(�U)���A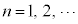 �ɑ��A
�ɑ��A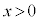 �ɂ����āA
�ɂ����āA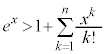 �@(�ؖ��I)
�@(�ؖ��I)
�ؖ������s�����̉E�ӂ́A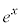 ���}�N���[�����W�J��n���ȉ��̎����̍��ł��B
���}�N���[�����W�J��n���ȉ��̎����̍��ł��B
�܂��A�s������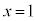 �Ƃ���ƁA
�Ƃ���ƁA
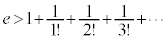
�ƂȂ�܂����A�E�ӂ̍ŏ���10���̘a�́A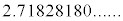 �ŁAe�̐^�̒l�ɂ��Ȃ�߂��l�ł��B
�ŁAe�̐^�̒l�ɂ��Ȃ�߂��l�ł��B
��2�D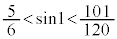
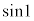 ��
��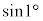 �ł͂Ȃ��A1[rad]�̐����̒l�ł��B
�ł͂Ȃ��A1[rad]�̐����̒l�ł��B
[�ؖ�]�@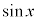 �̃}�N���[�����W�J�F
�̃}�N���[�����W�J�F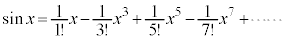 ��m���Ă���A�e���̕������l���āA
��m���Ă���A�e���̕������l���āA
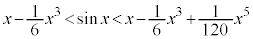 �Ƃ����s���������藧�������ł��B�܂��A���̕s�������ؖ����܂��B
�Ƃ����s���������藧�������ł��B�܂��A���̕s�������ؖ����܂��B
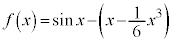 �Ƃ����ƁA
�Ƃ����ƁA
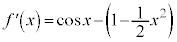
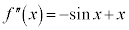
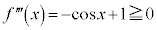
����āA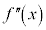 �͒P�������ł��B
�͒P�������ł��B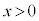 �ɂ����āA
�ɂ����āA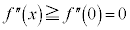
����āA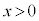 �ɂ����āA
�ɂ����āA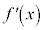 �͒P�������ł����āA
�͒P�������ł����āA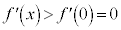
����āA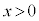 �ɂ����āA
�ɂ����āA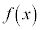 �͒P�������ł����āA
�͒P�������ł����āA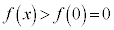
�� 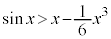 �@����@
�@����@
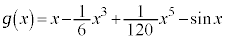 �Ƃ����ƁA
�Ƃ����ƁA
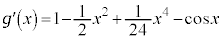
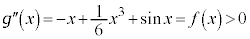 (
(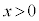 )
)
����āA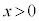 �ɂ����āA
�ɂ����āA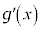 �͒P�������ł����āA
�͒P�������ł����āA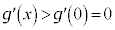
����āA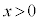 �ɂ����āA
�ɂ����āA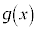 �͒P�������ł����āA
�͒P�������ł����āA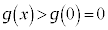
����āA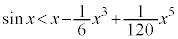 �@����A
�@����A
�@�C�A���A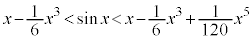
�����ŁA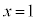 �Ƃ���ƁA
�Ƃ���ƁA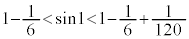
�� 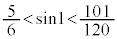 �@(�ؖ��I)
�@(�ؖ��I)
(2) �����𗘗p����s�����̏ؖ�
�Ⴆ�A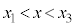 �ɂ�����
�ɂ�����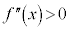 �ł����āA���͈̔͂�
�ł����āA���͈̔͂�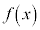 �����ɓʂ��Ƃ��܂��B
�����ɓʂ��Ƃ��܂��B
���̂Ƃ��A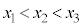 �ƂȂ�
�ƂȂ�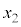 �ɂ��āA
�ɂ��āA
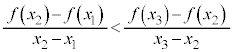
�����藧���܂��B
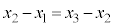 �̂Ƃ��A
�̂Ƃ��A
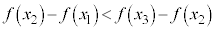
�� 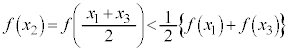
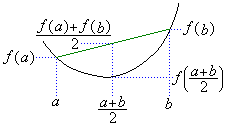 �����̓��ĂƂ��ẮA�킴�킴���ʂ̒�`�Ɉ˂�Ȃ��Ă��A
�����̓��ĂƂ��ẮA�킴�킴���ʂ̒�`�Ɉ˂�Ȃ��Ă��A
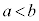 �Ƃ��āA
�Ƃ��āA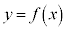 �̃O���t�����ɓʂȔ͈͂ɂ����āA�O���t���2�_
�̃O���t�����ɓʂȔ͈͂ɂ����āA�O���t���2�_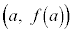 �C
�C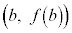 �����Ԑ����̓O���t�̏㑤��ʂ邩��A������̓_
�����Ԑ����̓O���t�̏㑤��ʂ邩��A������̓_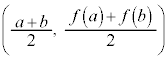 �́A
�́A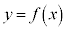 �̏㑤�ɂ���A
�̏㑤�ɂ���A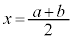 �ɂ�����O���t��̓_�Ɛ�����̓_��y���W�ɂ��āA
�ɂ�����O���t��̓_�Ɛ�����̓_��y���W�ɂ��āA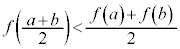
�Ɛ��������Ă����悢�ł��傤�B
��3.�D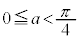 �C
�C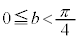 �̂Ƃ��A
�̂Ƃ��A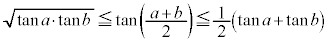 �@(���嗝�n'91�O��[4])
�@(���嗝�n'91�O��[4])
[�ؖ�]�@�E���̕s�����̕����Ղ����̂ŁA�����炩��ؖ����܂��B��L�̐����ŁA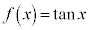 �Ƃ��������̂��̂ł��B
�Ƃ��������̂��̂ł��B
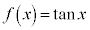 �Ƃ��āA
�Ƃ��āA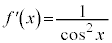 �C
�C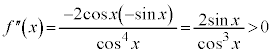 (
(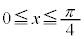 )
)
����āA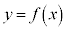 �̃O���t�͉��ɓʂŁA
�̃O���t�͉��ɓʂŁA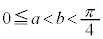 ���Ƃ��āA�O���t���2�_
���Ƃ��āA�O���t���2�_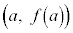 �C
�C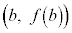 �����Ԑ�����
�����Ԑ�����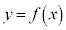 �̃O���t�̏㑤��ʂ邩��A������̓_
�̃O���t�̏㑤��ʂ邩��A������̓_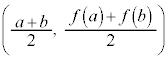 �́A
�́A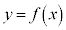 �̏㑤�ɂ���A
�̏㑤�ɂ���A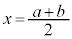 �ɂ�����O���t��̓_�Ɛ�����̓_��y���W�ɂ��āA
�ɂ�����O���t��̓_�Ɛ�����̓_��y���W�ɂ��āA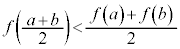 �@����@
�@����@
�� 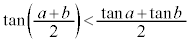 �@����A
�@����A
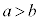 �̏ꍇ�����l�ŁA
�̏ꍇ�����l�ŁA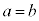 �Ȃ疾�炩�ɁA
�Ȃ疾�炩�ɁA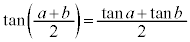 �@����B
�@����B
�A�C�B���A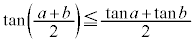 �@����C
�@����C
�����̕s�����ɂ��Ă����ʂ���ؖ��ł��Ȃ����A�ƁA�l���܂��B������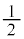 ��Ȃ̂ŁA����
��Ȃ̂ŁA����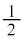 ���g���āA
���g���āA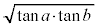 ��
��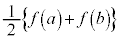 �̌`�Ƃ��邽�߂ɁA�����s�������ӂ̑ΐ����l���܂��B
�̌`�Ƃ��邽�߂ɁA�����s�������ӂ̑ΐ����l���܂��B
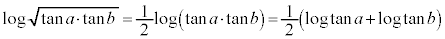
�]���āA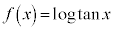 �Ƃ���悢���Ƃ��킩��܂��B
�Ƃ���悢���Ƃ��킩��܂��B
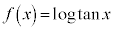 �́A
�́A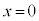 �ɂ����Ē�`�ł��Ȃ��̂ŁA
�ɂ����Ē�`�ł��Ȃ��̂ŁA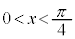 �͈̔͂ōl���܂��B
�͈̔͂ōl���܂��B
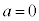 �C
�C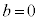 �̂�����ł����Ă��A���邢��
�̂�����ł����Ă��A���邢��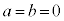 �ł����Ă��A
�ł����Ă��A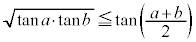 �@����D �͐������܂��B
�@����D �͐������܂��B
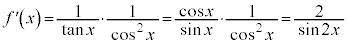
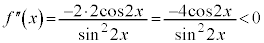 (
(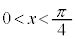 )
)
����āA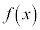 ��
��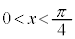 �ɂ����ď�ɓʂł��B�@�Ɠ��l�ɍl���āA
�ɂ����ď�ɓʂł��B�@�Ɠ��l�ɍl���āA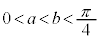 �̂Ƃ����x�́A
�̂Ƃ����x�́A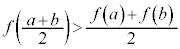 �ƂȂ�܂��B
�ƂȂ�܂��B
�� 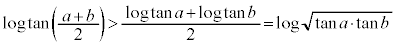
�� 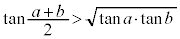 �@����E
�@����E
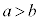 �̏ꍇ�����l�ŁA
�̏ꍇ�����l�ŁA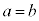 �Ȃ疾�炩�ɁA
�Ȃ疾�炩�ɁA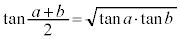 �@����F
�@����F
�D�C�E�C�F���A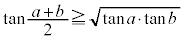 �@����G
�@����G
�C�C�G���A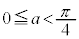 �C
�C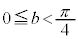 �̂Ƃ��A
�̂Ƃ��A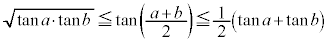 �@(�ؖ��I)
�@(�ؖ��I)
�����@�̕s�����ւ̉��p(2)����2�֑���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 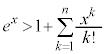
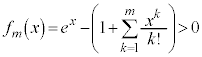 �����藧�Ɖ��肵�܂��B
�����藧�Ɖ��肵�܂��B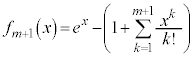 ���������ƁA
���������ƁA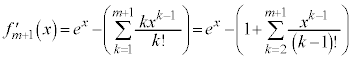
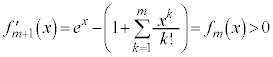 (
(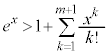
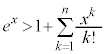 �@(�ؖ��I)
�@(�ؖ��I)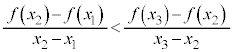
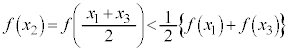
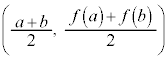 �́A
�́A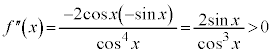 (
(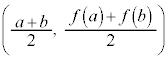 �́A
�́A