関数の増減 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
ある区間で定義された関数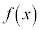 が、その区間内で
が、その区間内で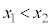 を満たす任意の
を満たす任意の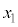 ,
,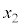 に対して、
に対して、
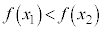 を満たすとき、
を満たすとき、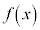 を増加関数と言う。
を増加関数と言う。
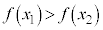 を満たすとき、
を満たすとき、 を減少関数と言う。
を減少関数と言う。
開区間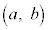 において微分可能な関数
において微分可能な関数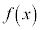 が、この区間において、
が、この区間において、
(i) 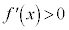 ならば、
ならば、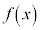 は増加関数
は増加関数
(ii) 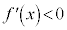 ならば、
ならば、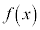 は減少関数
は減少関数
(iii) 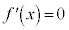 ならば、
ならば、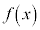 は定数関数
は定数関数
[証明] 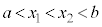 を満たす任意の
を満たす任意の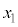 ,
,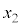 に対して、関数
に対して、関数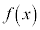 は、閉区間
は、閉区間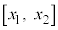 で連続、開区間
で連続、開区間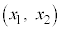 で微分可能だから、平均値の定理の要件を満たします。
で微分可能だから、平均値の定理の要件を満たします。
平均値の定理より、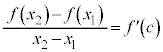 ,
,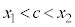 を満たすcが存在します。
を満たすcが存在します。
(i) 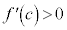 ならば、
ならば、 より、
より、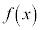 は増加関数です。
は増加関数です。
(ii) 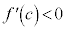 ならば、
ならば、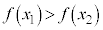 より、
より、 は減少関数です。
は減少関数です。
(iii) 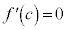 ならば、
ならば、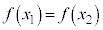 が、
が、 を満たす任意の
を満たす任意の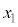 ,
,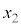 に対して成り立つので、
に対して成り立つので、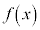 は定数です。 (証明終)
は定数です。 (証明終)
上記の事実によって、増減表で、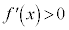 の区間に増加を表すマーク
の区間に増加を表すマーク を書き入れ、
を書き入れ、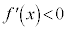 の区間に減少を表すマーク
の区間に減少を表すマーク を書き入れることになります。
を書き入れることになります。
例1 関数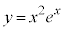 の増減を考えます。
の増減を考えます。
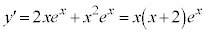
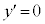 のとき、
のとき、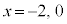
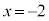 のとき
のとき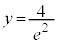 ,
,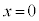 のとき
のとき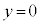
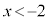 において
において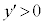 で増加,
で増加,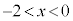 において
において で減少,
で減少,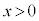 において
において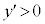 で増加となります。
で増加となります。
増減表は以下のようになります。
例2 関数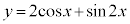 (
(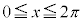 )の増減を考えます。
)の増減を考えます。
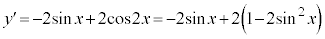
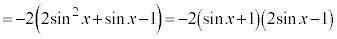
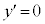 のとき、
のとき、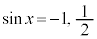 ,
,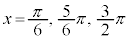
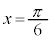 のとき
のとき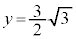 ,
,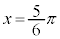 のとき
のとき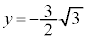 ,
,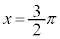 のとき
のとき
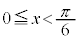 のとき
のとき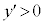 で増加、
で増加、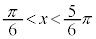 のとき
のとき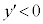 で減少、
で減少、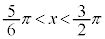 のとき
のとき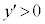 で増加、
で増加、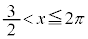 のとき
のとき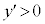 で増加となります。
で増加となります。
増減表は以下のようになります。
関数 が
が の前後で増加から減少に切り替わるとき、
の前後で増加から減少に切り替わるとき、 は
は において極大であると言います。また
において極大であると言います。また を極大値と言います。
を極大値と言います。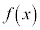 が
が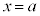 で極大であっても
で極大であっても になるとは言えません。
になるとは言えません。
関数 が
が の前後で減少から増加に切り替わるとき、
の前後で減少から増加に切り替わるとき、 は
は において極小であると言います。また
において極小であると言います。また を極小値と言います。
を極小値と言います。 が
が で極小であっても
で極小であっても になるとは言えません。
になるとは言えません。
極大値と極小値を合わせて極値と言います。
極値を求める場合、通常は となるところを探しますが、
となるところを探しますが、 が存在しないようなところでも極大・極小になることがあります。
が存在しないようなところでも極大・極小になることがあります。
上記の例1においては、関数 は、
は、 において極大で、
において極大で、 において極小です。
において極小です。 において極大値
において極大値 をとり、
をとり、 で極小値0をとります。
で極小値0をとります。
上記の例2においては、関数 は、
は、 において極大で、
において極大で、 において極大値
において極大値 をとり、
をとり、 において極小で、
において極小で、 において極小値
において極小値 をとります。
をとります。 において
において ですが、このときのyの値0は極値とは言いません。
ですが、このときのyの値0は極値とは言いません。 においては極大でも極小でもありません。
においては極大でも極小でもありません。
例3 関数 は、
は、 の前後で減少から増加に切り替わるので、
の前後で減少から増加に切り替わるので、 において極小で、極小値0をとります。また、
において極小で、極小値0をとります。また、 の前後で減少から増加に切り替わるので、
の前後で減少から増加に切り替わるので、 においても極小で、極小値0をとります。ですが、
においても極小で、極小値0をとります。ですが、 ,
, においては微分係数は存在しません。
においては微分係数は存在しません。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。なお、解答は、
苦学楽学塾制作です。©2005-2025(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 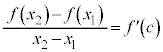 ,
,