���ϒl�̒藝�@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���[��(Rolle)�̒藝�F��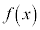 ���A���
���A���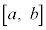 �ɂ������A�����A�J���
�ɂ������A�����A�J���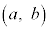 �ɂ����������\�ȂƂ��A
�ɂ����������\�ȂƂ��A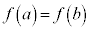 �����藧�Ȃ�A
�����藧�Ȃ�A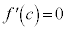 �C
�C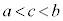 ����c�����݂���B
����c�����݂���B
[�ؖ�]�@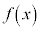 ��
��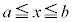 �ɂ����ĘA��������A�ő�l�E�ŏ��l�̒藝�ɂ��A���͈̔͂ɍő�l�A�ŏ��l�������܂��B
�ɂ����ĘA��������A�ő�l�E�ŏ��l�̒藝�ɂ��A���͈̔͂ɍő�l�A�ŏ��l�������܂��B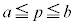 �C
�C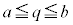 �Ƃ��āA
�Ƃ��āA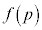 ���ő�l�A
���ő�l�A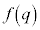 ���ŏ��l���Ƃ��܂��B
���ŏ��l���Ƃ��܂��B
�E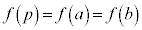 �̂Ƃ��A�ŏ��l�͍ő�l�ȉ��Ȃ̂�
�̂Ƃ��A�ŏ��l�͍ő�l�ȉ��Ȃ̂�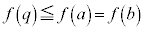 �ł��B
�ł��B 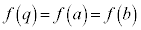 �Ȃ�A
�Ȃ�A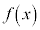 ��
��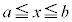 �ɂ����Ă˂�
�ɂ����Ă˂�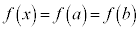 (
(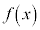 �͒萔��)�Ƃ������ƂȂ̂ŁA
�͒萔��)�Ƃ������ƂȂ̂ŁA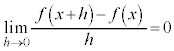 �C�܂�A
�C�܂�A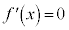 �ł���A
�ł���A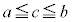 �����C�ӂ�c�ɂ��āA
�����C�ӂ�c�ɂ��āA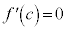 �ł��B
�ł��B
�E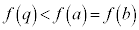 ���Ƃ��܂��B
���Ƃ��܂��B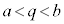 �ł��B
�ł��B 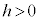 �C
�C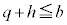 �̂Ƃ��A
�̂Ƃ��A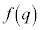 ���ŏ��l�Ȃ̂ŁA
���ŏ��l�Ȃ̂ŁA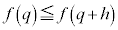 �ł����āA
�ł����āA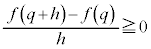
�� 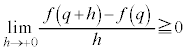 �@����@
�@����@
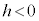 �C
�C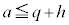 �̂Ƃ��A
�̂Ƃ��A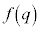 ���ŏ��l�Ȃ̂ŁA
���ŏ��l�Ȃ̂ŁA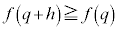 �ł����āA
�ł����āA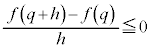 �@(
�@(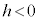 �ɒ���)��
�ɒ���)�� 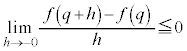 �@����A
�@����A
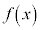 �͔����\�Ȃ̂ŁA�@�C�A���A
�͔����\�Ȃ̂ŁA�@�C�A���A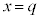 �ɂ����āA
�ɂ����āA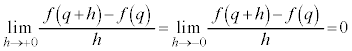
�� 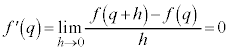 ����āA
����āA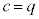 �Ƃ���A
�Ƃ���A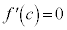 �C
�C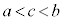 ����c�����݂��܂��B
����c�����݂��܂��B
�E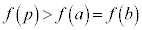 �̂Ƃ��A
�̂Ƃ��A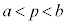 �ł��B
�ł��B 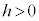 �C
�C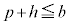 �̂Ƃ��A
�̂Ƃ��A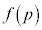 ���ő�l�Ȃ̂ŁA
���ő�l�Ȃ̂ŁA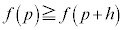 �ł����āA
�ł����āA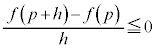
�� 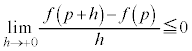 �@����@
�@����@
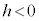 �C
�C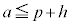 �̂Ƃ��A
�̂Ƃ��A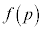 ���ő�l�Ȃ̂ŁA
���ő�l�Ȃ̂ŁA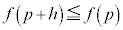 �ł����āA
�ł����āA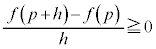 �@(
�@(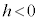 �ɒ���)��
�ɒ���)�� 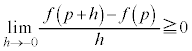 �@����A
�@����A
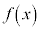 �͔����\�Ȃ̂ŁA
�͔����\�Ȃ̂ŁA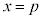 �ɂ����āA
�ɂ����āA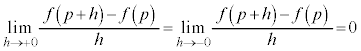 �@(�� �@�C�A)��
�@(�� �@�C�A)�� 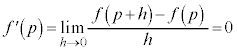 ����āA
����āA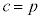 �Ƃ���A
�Ƃ���A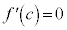 �C
�C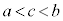 ����c�����݂��܂��B
����c�����݂��܂��B
�ȏ���A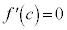 �C
�C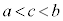 ����c�����݂��܂��B�@(�ؖ��I)
����c�����݂��܂��B�@(�ؖ��I)
���O�����W��(Lagrange)�����ϒl�̒藝�F��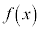 ���A���
���A���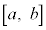 �ɂ������A�����A�J���
�ɂ������A�����A�J���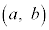 �ɂ����������\�ȂƂ��A
�ɂ����������\�ȂƂ��A
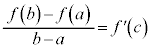 �C
�C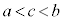
���D���̒藝���A���Z�̋��ȏ��E�Q�l���Ɂu���ϒl�̒藝�v�Ƃ��čڂ��Ă���藝�ł��B
[�ؖ�]�@���F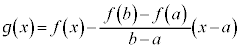 �́A���
�́A���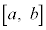 �ɂ����ĘA�����A�J���
�ɂ����ĘA�����A�J���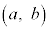 �ɂ����Ĕ����\�Ȋ��ł���A
�ɂ����Ĕ����\�Ȋ��ł���A
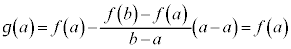 �C
�C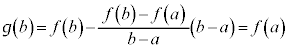 ���A
���A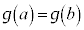
����āA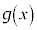 �̓��[���̒藝�̗v�������̂ŁA���[���̒藝���A
�̓��[���̒藝�̗v�������̂ŁA���[���̒藝���A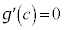 �C
�C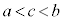 ����c�����݂��܂��B
����c�����݂��܂��B
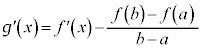 ���A
���A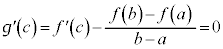 �̂Ƃ��A
�̂Ƃ��A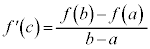
����āA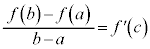 �C
�C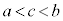 ����c�����݂��܂��B�@(�ؖ��I)
����c�����݂��܂��B�@(�ؖ��I)
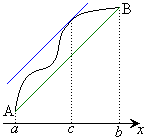 ���ϒl�̒藝�̍��ӂ́A
���ϒl�̒藝�̍��ӂ́A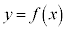 �̃O���t���2�_A
�̃O���t���2�_A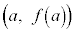 �CB
�CB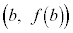 �����Ԓ����̌X���ŁA���ϕω����ł��B
�����Ԓ����̌X���ŁA���ϕω����ł��B
 �Ƃ����͈͂̒��ŗ��[�����Ԓ���AB�ƕ��s�Ȑڐ������͈̔͂̒��̂ǂ����ň������Ƃ��ł���A�Ƃ����̂��A���ϒl�̒藝�̎��o�I�Ӗ��ł��B�o����Ƃ��́A�������Ŋo���Ȃ��ŁA���o�I�Ӗ��̕����o���܂��傤�B
�Ƃ����͈͂̒��ŗ��[�����Ԓ���AB�ƕ��s�Ȑڐ������͈̔͂̒��̂ǂ����ň������Ƃ��ł���A�Ƃ����̂��A���ϒl�̒藝�̎��o�I�Ӗ��ł��B�o����Ƃ��́A�������Ŋo���Ȃ��ŁA���o�I�Ӗ��̕����o���܂��傤�B
��D�s�����F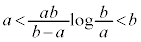 �������B
�������B
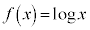 ��
��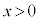 �ɂ����������\�Ȋ��B
�ɂ����������\�Ȋ��B
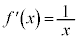
���ϒl�̒藝���A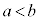 �Ƃ��āA
�Ƃ��āA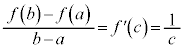 �C
�C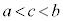 ����c�����݂���B
����c�����݂���B
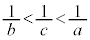 ���A
���A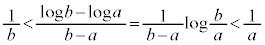
�� 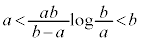
�R�[�V�[(Cauchy)�̕��ϒl�̒藝�F��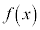 �C
�C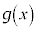 ���A���
���A���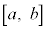 �ɂ����ĘA�����A�J���
�ɂ����ĘA�����A�J���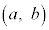 �ɂ����������\�ŁA
�ɂ����������\�ŁA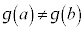 �C
�C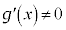 �ł���Ƃ��A
�ł���Ƃ��A
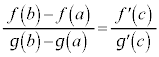 �C
�C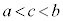
����c�����݂���B
[�ؖ�]�@���F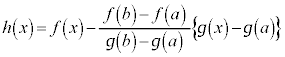 �́A���
�́A���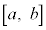 �ɂ����ĘA�����A�J���
�ɂ����ĘA�����A�J���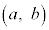 �ɂ����Ĕ����\�Ȋ��ł���A
�ɂ����Ĕ����\�Ȋ��ł���A
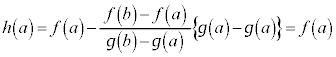 �C
�C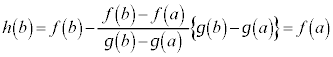 ���A
���A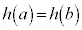
����āA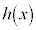 �̓��[���̒藝�̗v�������̂ŁA���[���̒藝���A
�̓��[���̒藝�̗v�������̂ŁA���[���̒藝���A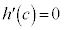 �C
�C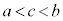 ����c�����݂��܂��B
����c�����݂��܂��B
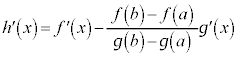 ���A
���A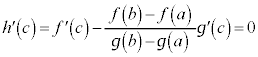 �̂Ƃ��A
�̂Ƃ��A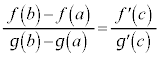
����āA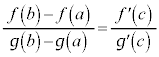 �C
�C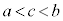 ����c�����݂��܂��B�@(�ؖ��I)
����c�����݂��܂��B�@(�ؖ��I)
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 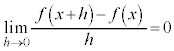 �C�܂�A
�C�܂�A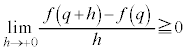 �@����@
�@����@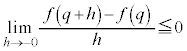 �@����A
�@����A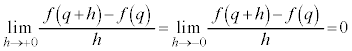
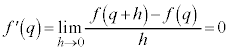
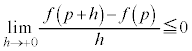 �@����@
�@����@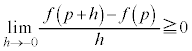 �@����A
�@����A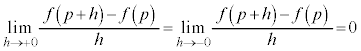 �@(�� �@�C�A)
�@(�� �@�C�A)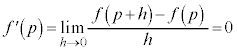
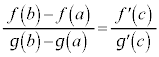 �C
�C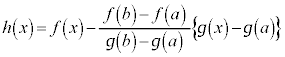 �́A���
�́A���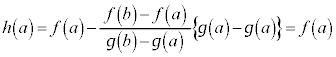 �C
�C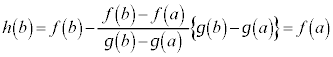 ���A
���A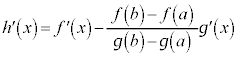 ���A
���A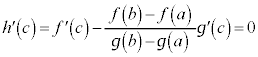 �̂Ƃ��A
�̂Ƃ��A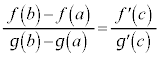
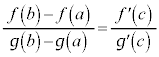 �C
�C