最大値・最小値の定理
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
最大値・最小値の定理：閉区間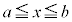
において連続な関数
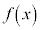は、その区間内で最大値、最小値をもつ。
詳細な証明は専門的になるので省略します。
(i) 閉区間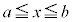
で連続ということは、
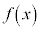が区間内のすべての実数xで定義されているということなので、
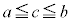となる
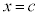において、
‘
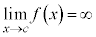'というようなことはありません。
‘
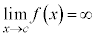'となるようなcがあるなら、
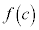が定義されないということだからです。
(ii) また、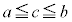
となる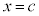
において、‘閉区間
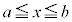内のすべての実数xについて
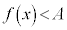，かつ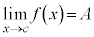
'を満たす実数Aは存在しません。
なぜなら、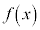
は連続なので
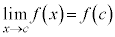であって、
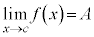なら、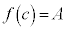
であり、閉区間
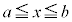内のすべてのxについて
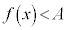であることに矛盾してしまうからです。
(i)，(ii)より、‘閉区間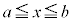
内のすべての実数xについて
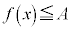，かつ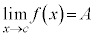
'を満たす実数
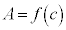が存在して、このAが閉区間
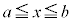における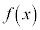
の最大値です。
同様に、最小値の存在を考えることができます。
なお、開区間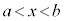
においては、
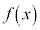がこの区間で単調増加な場合には、
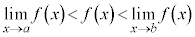であって、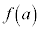
，
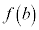がそもそも定義されないか、されたとしても、
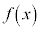が値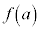
，
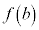をとらないので、最大値、最小値をもつとは限りません。
開区間の場合には、最大値、最小値をもつ場合もありますが、どちらか、あるいは、両方とも、もたない、ということがあり得ます。
例．3次関数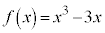
は、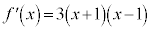
，
，
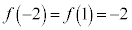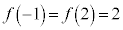より、増減表は以下の通り。
増減表より、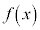
は、全実数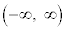
においては、最大値、最小値をもちません。開区間
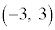においても最大値、最小値をもちません。
閉区間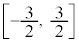
では、最大値
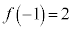、最小値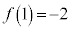
をもちます。
閉区間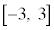
においては、最大値
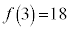，最小値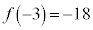
をもちます。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
