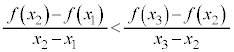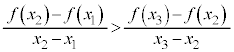関数の凹凸 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
ある区間で定義された関数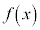 が、その区間内で
が、その区間内で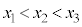 を満たす任意の
を満たす任意の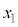 ,
,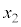 ,
,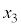 に対して、
に対して、
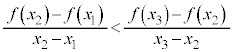 を満たすとき、
を満たすとき、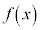 は下に凸であると言う。
は下に凸であると言う。
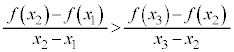 を満たすとき、
を満たすとき、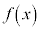 は上に凸であると言う。
は上に凸であると言う。
開区間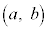 において2回微分可能な関数
において2回微分可能な関数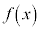 が、この区間において、
が、この区間において、
(i) 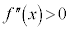 ならば、
ならば、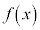 は下に凸
は下に凸
(ii) 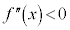 ならば、
ならば、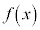 は上に凸
は上に凸
[証明] 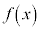 は、閉区間
は、閉区間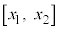 において連続、開区間
において連続、開区間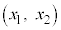 において微分可能なので平均値の定理の要件を満たします。平均値の定理より、
において微分可能なので平均値の定理の要件を満たします。平均値の定理より、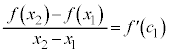 ,
,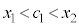 を満たす
を満たす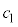 が存在します。
が存在します。
また、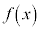 は、閉区間
は、閉区間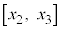 において連続、開区間
において連続、開区間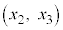 において微分可能なので平均値の定理の要件を満たします。平均値の定理より、
において微分可能なので平均値の定理の要件を満たします。平均値の定理より、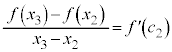 ,
,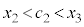 を満たす
を満たす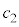 が存在します。
が存在します。
(i) 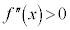 なら
なら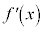 は増加関数なので、
は増加関数なので、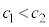 より、
より、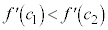 です。
です。
∴ 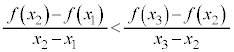
よって、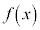 は下に凸です。
は下に凸です。
(ii) 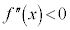 なら
なら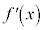 は減少関数なので、
は減少関数なので、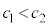 より、
より、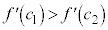 です。
です。
∴ 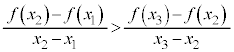
よって、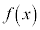 は上に凸です。
は上に凸です。
(証明終)
上に凸、下に凸をまとめて凹凸と言います。
上記の凹凸の定義に出てくる不等式の両辺は、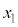 から
から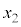 までの平均変化率と、
までの平均変化率と、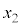 から
から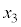 までの平均変化率です。
までの平均変化率です。
平均変化率がだんだん増加するときに下に凸で、だんだん減少するときに下に凸です。
上記の証明の途中で、
(i)の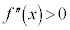 の場合には、
の場合には、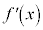 が増加すると書きましたが、これは、接線の傾きが増加する(接線が右下がりから右上がりになる)ときに下に凸になると言うことです。
が増加すると書きましたが、これは、接線の傾きが増加する(接線が右下がりから右上がりになる)ときに下に凸になると言うことです。
(ii)の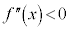 の場合には、
の場合には、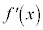 が減少し、接線の傾きが減少する(接線が右上がりから右下がりになる)ときに上に凸になります。
が減少し、接線の傾きが減少する(接線が右上がりから右下がりになる)ときに上に凸になります。
曲線上で、凹凸が変化する点、つまり、下に凸から上に凸に切り替わる点、あるいは、上に凸から下に凸に切り替わる点を、変曲点と言います。
変曲点の前後で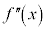 の符号が+から−へ、あるいは、−から+へ切り替わります。
の符号が+から−へ、あるいは、−から+へ切り替わります。
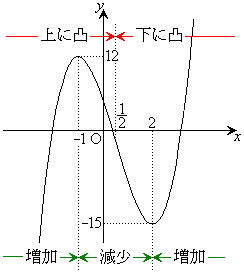 例.
例.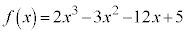 の増減と凹凸を調べる。
の増減と凹凸を調べる。
[解答] 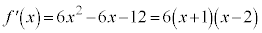
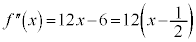
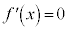 とすると、
とすると、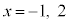
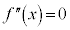 とすると、
とすると、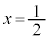
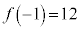 ,
,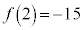 ,
,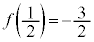
変曲点は、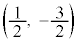 です。
です。
増減表は以下の通り
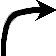 は、
は、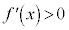 ,
,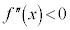 で、上に凸で増加することを表します。
で、上に凸で増加することを表します。
 は、
は、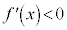 ,
,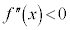 で、上に凸で減少することを表します。
で、上に凸で減少することを表します。
 は、
は、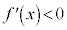 ,
,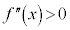 で、下に凸で減少することを表します。
で、下に凸で減少することを表します。
 は、
は、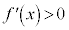 ,
,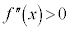 で、上に凸で増加することを表します。
で、上に凸で増加することを表します。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 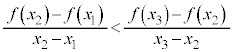 を満たすとき、
を満たすとき、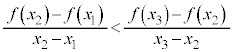 を満たすとき、
を満たすとき、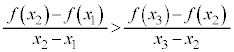 を満たすとき、
を満たすとき、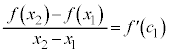 ,
,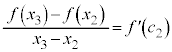 ,
,