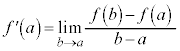�ڐ��Ɣ����W���@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�����W���E�����̏ڍׂɂ��ẮA�����E�������Q�ƁB
 ��
��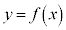 �̃O���t���2�_
�̃O���t���2�_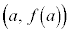 �C
�C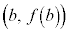 �����Ԓ����̌X��
�����Ԓ����̌X��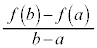 �����ϕω����ƌ����܂��B
�����ϕω����ƌ����܂��B
�����ŁAb������Ȃ�a�ɋ߂Â���ƁA2�_�����Ԓ����́A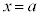 �ɂ�����ڐ��Ɍ���Ȃ��߂Â��A�����̌X��
�ɂ�����ڐ��Ɍ���Ȃ��߂Â��A�����̌X��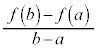 �́A����Ȃ�
�́A����Ȃ�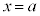 �ɂ�����ڐ��̌X���ɋ߂Â��Ă����܂��B
�ɂ�����ڐ��̌X���ɋ߂Â��Ă����܂��B
b������Ȃ�a�ɋ߂Â���Ƃ��A���ϕω���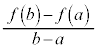 ������Ȃ��߂Â��l������W���ƌ����A
������Ȃ��߂Â��l������W���ƌ����A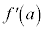 �Ə����܂��B�����A
�Ə����܂��B�����A
�����W��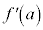 �́A
�́A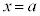 �ɂ�����ڐ��̌X����\���܂��B
�ɂ�����ڐ��̌X����\���܂��B
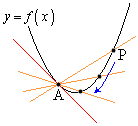
�]���āA��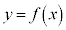 �̃O���t��
�̃O���t��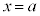 �ɂ�����ڐ��́A�_
�ɂ�����ڐ��́A�_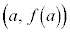 ��ʂ�A�X��
��ʂ�A�X��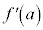 �̒������Ƃ���(�����̕��������Q��)�A
�̒������Ƃ���(�����̕��������Q��)�A
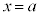 �ɂ�����
�ɂ�����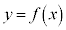 �̐ڐ��F
�̐ڐ��F
�ƕ\�����Ƃ��ł��܂��B
��1�D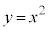 ��
��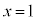 �ɂ�����ڐ������߂�B
�ɂ�����ڐ������߂�B
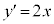 �C
�C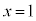 �̂Ƃ��A
�̂Ƃ��A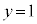 �C
�C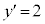 ���A
���A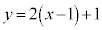
�� �ڐ��F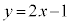
��2�D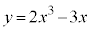 ��
��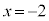 �ɂ�����ڐ������߂�B
�ɂ�����ڐ������߂�B
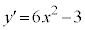
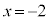 �̂Ƃ��A
�̂Ƃ��A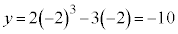 �C
�C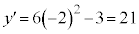 ���A
���A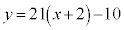
�� �ڐ��F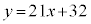
��3�D�Ȑ��F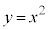 �ɁA�_
�ɁA�_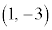 ����������ڐ������߂�B
����������ڐ������߂�B
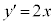
�ړ_��x���W��t�Ƃ��āA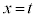 �̂Ƃ��A
�̂Ƃ��A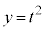 �C
�C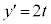 ���A
���A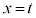 �ɂ�����ڐ��́A
�ɂ�����ڐ��́A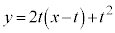
�������āA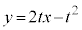 �@����@
�@����@
�ڐ��͓_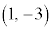 ��ʂ邩��A�@�ɂ����āA
��ʂ邩��A�@�ɂ����āA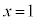 �C
�C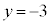 �Ƃ���ƁA
�Ƃ���ƁA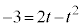
�� 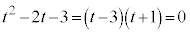
�� 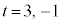
�@�ɂ����āA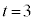 �Ƃ��āA
�Ƃ��āA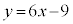
�@�ɂ����āA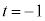 �Ƃ��āA
�Ƃ��āA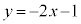
���߂�ڐ��́A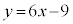 �C
�C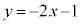 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B