�����̕������@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���W���ʏ�ɂ����āA
�X��m�Cy�ؕ�n�̒����̕������F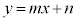
�_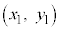 ��ʂ�A�X��m�̒����̕������F
��ʂ�A�X��m�̒����̕������F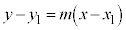
�قȂ�2�_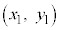 �C
�C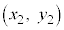 ��ʂ钼���̕������F
��ʂ钼���̕������F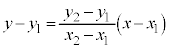 (�A���A
(�A���A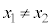 )
)
�قȂ�2�_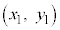 �C
�C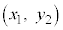 ��ʂ钼���̕������́A
��ʂ钼���̕������́A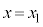
 1�����F
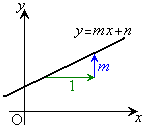
1�����F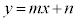 �̃O���t�͒����ł��B
�̃O���t�͒����ł��B
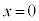 �Ƃ���ƁA
�Ƃ���ƁA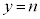 �ɂȂ�̂ŁAy���Ƃ̌�_��
�ɂȂ�̂ŁAy���Ƃ̌�_��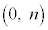 �ɂȂ�܂��B
�ɂȂ�܂��B
�X����m�Ƃ������Ƃ́A�E�}�̂悤�ɁAx������1�i�ނƁAy������m�i�ނƂ����Ӗ��ł��B
�����F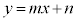 ��x���Ƃ̂Ȃ��p��x�����甽���v���ɒ����܂ő������p��θ�Ƃ���ƁA
��x���Ƃ̂Ȃ��p��x�����甽���v���ɒ����܂ő������p��θ�Ƃ���ƁA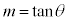 �ɂȂ�܂��B
�ɂȂ�܂��B
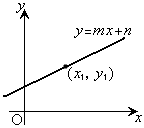 �����F
�����F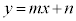 ����@ ���A�_
����@ ���A�_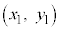 ��ʂ�Ƃ��A
��ʂ�Ƃ��A
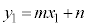 ����A ���A
����A ���A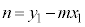
�@�ɑ������ƁA
�� 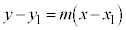
�܂�A�_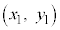 ��ʂ�A�X��m�̒����̕������́A
��ʂ�A�X��m�̒����̕������́A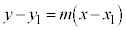 ����B
����B
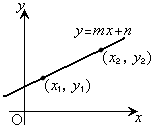 �����B���A����ɁA�_
�����B���A����ɁA�_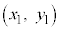 �ƈقȂ�_
�ƈقȂ�_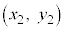 ��ʂ�Ƃ��A
��ʂ�Ƃ��A
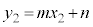 ����C
����C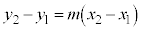
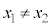 �ł���A
�ł���A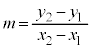 �F�����̌X��
�F�����̌X��
�B�ɑ�����āA2�_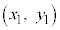 �C
�C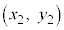 ��ʂ钼���̕������́A
��ʂ钼���̕������́A
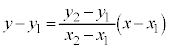 (�A���A
(�A���A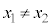 ) ����D
) ����D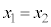 �̏ꍇ�́A�����̕�������
�̏ꍇ�́A�����̕�������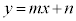 �̌`�ɏ������Ƃ��ł��܂���B���ƂŁA�l�@���܂��B
�̌`�ɏ������Ƃ��ł��܂���B���ƂŁA�l�@���܂��B
�D�̕�����ƁA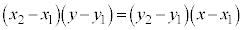
�������āA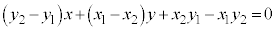
�����ŁA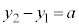 �C
�C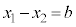 �C
�C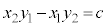 �Ƃ����ƁA
�Ƃ����ƁA
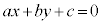 ����E
����E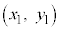 �Ɠ_
�Ɠ_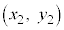 ���قȂ�2�_�Ƃ����̂ŁA
���قȂ�2�_�Ƃ����̂ŁA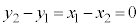 �C�܂�A
�C�܂�A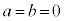 �ɂȂ邱�Ƃ͂���܂���B
�ɂȂ邱�Ƃ͂���܂���B
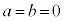 �łȂ���A�E��������\���������ł��B
�łȂ���A�E��������\���������ł��B
�D�ł́A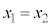 �̏ꍇ���������Ƃ��ł��܂���ł����B
�̏ꍇ���������Ƃ��ł��܂���ł����B
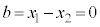 �̂Ƃ��A�E�́A
�̂Ƃ��A�E�́A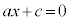 �ƂȂ�܂��B
�ƂȂ�܂��B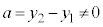 �Ȃ̂ŁA
�Ȃ̂ŁA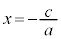
�܂�A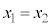 �̏ꍇ�́A�����̕������́A�e
�̏ꍇ�́A�����̕������́A�e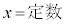 ' �̌`�ɂȂ�܂��B
' �̌`�ɂȂ�܂��B
�_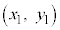 �C
�C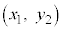 ��ʂ钼���̕������́A
��ʂ钼���̕������́A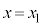
�����̕������́A�z���\���F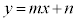 �ƁA�A���\���F
�ƁA�A���\���F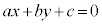 ��2�ʂ肪�\�Ȃ̂ł����A
��2�ʂ肪�\�Ȃ̂ł����A
�z���\���́Ax�Cy�ȊO�̕�����m�Cn��2���������Ȃ��̂ɑ��āA�A���\���́Aa�Cb�Cc��3���̂ŁA�A���\���̕������R�x���傫���̂ł��B
���ɁA�z���\���ł́Ax���ɐ����Ȓ���(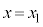 �Ƃ����`�����Ă��܂�)��\�����Ƃ��ł��܂���B
�Ƃ����`�����Ă��܂�)��\�����Ƃ��ł��܂���B
�������������Ƃ��ɁA���W���ʏ�ŁA���ň��������Ƃ���x���ɐ����Ȓ������܂ނ̂ł���A�A���\�����g���A�܂܂Ȃ��̂ł���A�z���\�����g���̂��悢�ł��傤�B
�_�ƒ����̋����̌�����p����Ƃ��ɂ́A�A���\�����g���܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B