二項定理の応用 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
二項定理：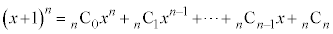
･･･① において、
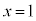とおくと、
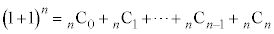より、
公式： |
が得られます。
①において、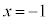
とおくと、
nが偶数のときには、
∴ 
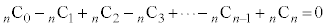
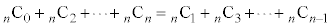
nが奇数のときには、
∴ 
，
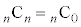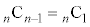などにより、①は、
･･･②
とも書けます。
②を微分すると、
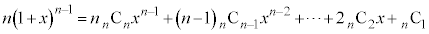･･･③
ここで、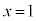
とおくと、
②を0から1まで積分すると、
∴ 
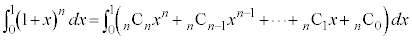
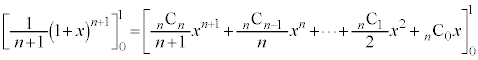
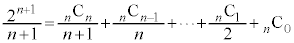
二項定理：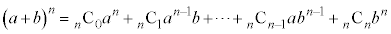
をbについて微分すると、
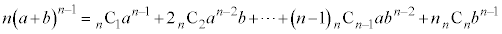
両辺にbをかけて、
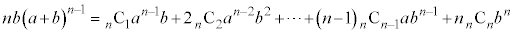
ここで、
とすると、
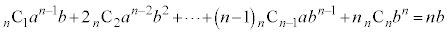･･･④
左辺の第k項目(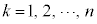
)に出てくる、
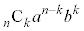は、1回の試行で事象Eの起こる確率がbだとするとき、n回試行を行ったうちk回事象Aが起こる確率(反復試行の確率)です。④の左辺は、これにkをかけて、
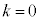から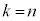
まで足し合わせたものになっているので、k回事象Aが起こったときに得点kがもらえるとしたとき(Aが1回も起こらなかったときは得点0)の得点の期待値を表しており、④は、この期待値が
であることを意味しています。
例えば、サイコロを300回振って、1の目が出た(確率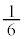
)回数だけ得点をもらえるとしたときの得点の期待値は、
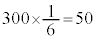点です。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。