二項定理 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
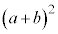 の展開において、
の展開において、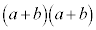 の左側の
の左側の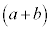 からa,右側の
からa,右側の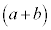 からaをとってかけると
からaをとってかけると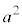 となり、左側の
となり、左側の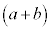 からa,右側の
からa,右側の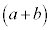 からbをとると
からbをとると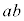 ,左側の
,左側の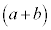 からb,右側の
からb,右側の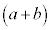 からaをとると
からaをとると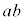 ,左側の
,左側の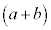 からb,右側の
からb,右側の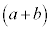 からbをとると
からbをとると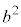 という項が得られます。
という項が得られます。
結局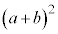 の展開からは、
の展開からは、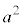 は2つの
は2つの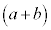 から0個のbを選ぶ組み合わせ
から0個のbを選ぶ組み合わせ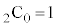 個,
個,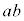 は2つの
は2つの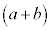 から1個のbを選ぶ組み合わせ
から1個のbを選ぶ組み合わせ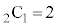 個,
個,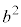 は2つの
は2つの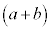 から2個のbを選ぶ組み合わせ
から2個のbを選ぶ組み合わせ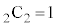 個の項が出てくるので、
個の項が出てくるので、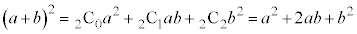 となります。
となります。
同様にして、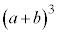 の展開において、
の展開において、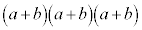 の3つの
の3つの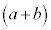 から0個のbを選んでかければ
から0個のbを選んでかければ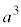 ,1個のbを選べば
,1個のbを選べば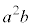 ,2個のbを選べば
,2個のbを選べば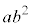 ,3個のbを選べば
,3個のbを選べば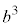 という項が得られるので、
という項が得られるので、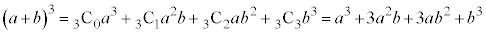 となります。
となります。
一般に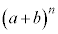 の展開においては、n個の
の展開においては、n個の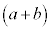 からk個(
からk個(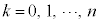 )のbを選ぶとき
)のbを選ぶとき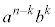 という項ができるので、
という項ができるので、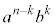 という項は
という項は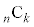 個できることになります。従って、以下の二項定理が成立します。
個できることになります。従って、以下の二項定理が成立します。
(1) 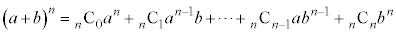
(2) 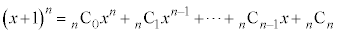
(1)は、Σ記号を使って書くと、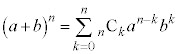 となります。
となります。
(1)において、aをx,bを1とすれば、(2)が得られます。(2)をΣ記号を使って書くと、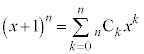 となります。
となります。
例.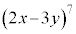 を展開したときの
を展開したときの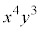 の項の係数を求めます。
の項の係数を求めます。
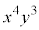 の項は、7個の
の項は、7個の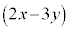 から
から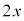 を4個、
を4個、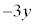 を3個選んでかけると得られます。従って、
を3個選んでかけると得られます。従って、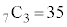 個の項ができるので、この項は、
個の項ができるので、この項は、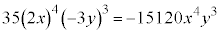 となり、係数は、
となり、係数は、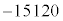 です。
です。
なお、二項定理の応用を参照してください。
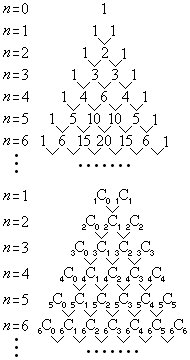
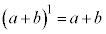
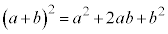
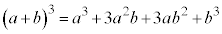
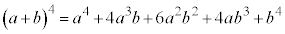
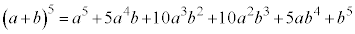
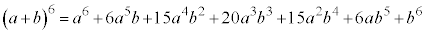
・・・・・・
の係数を並べた表を右上図に示します。これをパスカルの三角形と言います。
これは、右下図のように、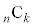 を各nについて、
を各nについて、 として計算したものを並べたものです。
として計算したものを並べたものです。
従って、右上図の左右の端は、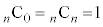 になります。また、\/の上2つの数を足すと下の数になります(パスカルの三角形を作るときはこの性質を利用して作ります)が、これは、公式:
になります。また、\/の上2つの数を足すと下の数になります(パスカルの三角形を作るときはこの性質を利用して作ります)が、これは、公式: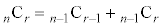 を意味しています。例えば、
を意味しています。例えば、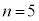 の段の
の段の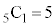 と
と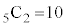 を加えると、
を加えると、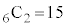 となりますが、
となりますが、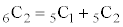 を意味しています。
を意味しています。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 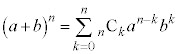 となります。
となります。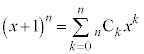 となります。
となります。