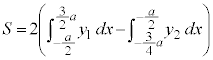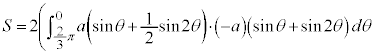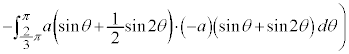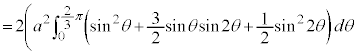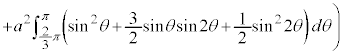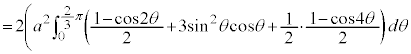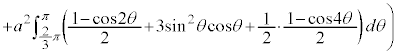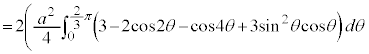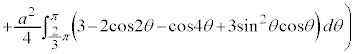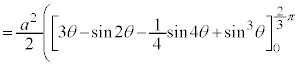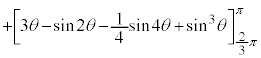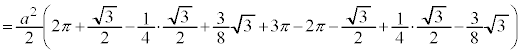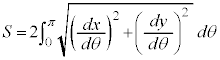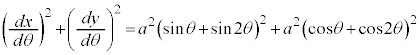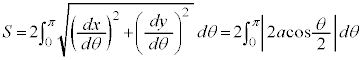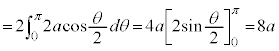カージオイド 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
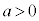 として、
として、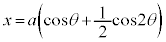 ,
,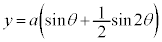 (
(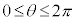 ) で与えられる曲線をカージオイドと言う。
) で与えられる曲線をカージオイドと言う。
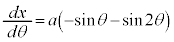 ,
,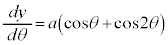 ,
,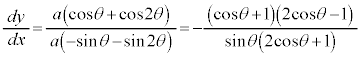 (媒介変数表示された関数の微分法を参照)
(媒介変数表示された関数の微分法を参照)
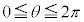 における増減表は以下の通りです。
における増減表は以下の通りです。
| θ | 0 |
| 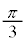 |
| 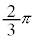 |
| θ |
| 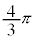 |
| 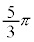 |
| 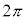 |
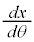 | 0 | − | − | − | 0 | + | 0 | − | 0 | + | + | + | 0 |
| x | 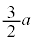 |  | 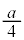 |  | 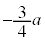 |  | 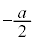 |  | 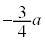 |  | 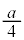 |  | 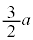 |
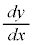 | × | − | 0 | + | × | − | × | + | × | − | 0 | + | × |
| y | 0 |  | 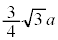 |  | 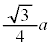 |  | 0 |  | 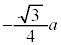 |  | 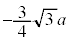 |  | 0 |
注.増減表でyの変化がおかしいと思うかも知れません。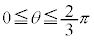 においては、xはθ に対して単調減少なので、上の増減表ではxの欄から下を右から左に見ていく必要があります。
においては、xはθ に対して単調減少なので、上の増減表ではxの欄から下を右から左に見ていく必要があります。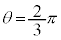 から
から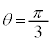 まででxは
まででxは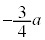 から
から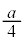 まで変化し、yは
まで変化し、yは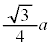 から
から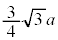 まで増加するので、
まで増加するので、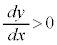 になっています。
になっています。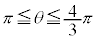 においても同様に、xの欄から下を右から左に見ていく必要があります。
においても同様に、xの欄から下を右から左に見ていく必要があります。
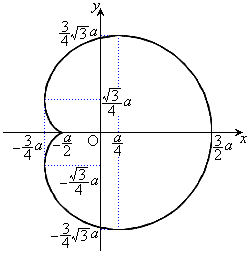 グラフは右図のようになります。
グラフは右図のようになります。
右図のカージオイドCで囲まれる部分の面積Sを求めてみます。
グラフはx軸に関して対称なので、x軸から上の部分を2倍して求めることにします。
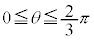 に対応する部分を
に対応する部分を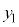 ,
,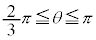 に対応する部分を
に対応する部分を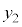 とすると、面積を求める部分は、
とすると、面積を求める部分は、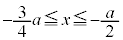 においては、
においては、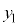 と
と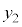 で挟まれる部分、
で挟まれる部分、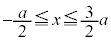 においては、
においては、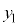 とx軸に挟まれた部分になります。従って、Sは、
とx軸に挟まれた部分になります。従って、Sは、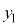 について
について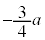 から
から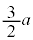 まで積分したものから、
まで積分したものから、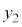 について
について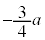 から
から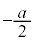 まで積分したものを引けば求められます。
まで積分したものを引けば求められます。
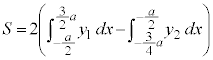
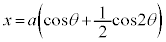 とおいて置換積分すると、
とおいて置換積分すると、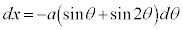
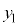 について、x:
について、x: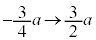 のとき、θ:
のとき、θ: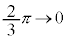
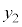 について、x:
について、x: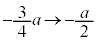 のとき、θ:
のとき、θ: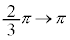
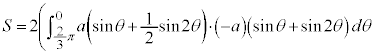
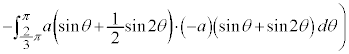
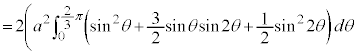
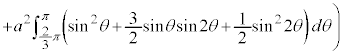
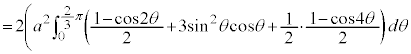
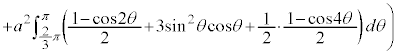
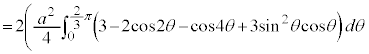
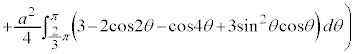
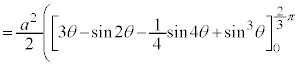
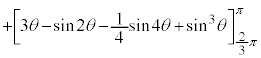
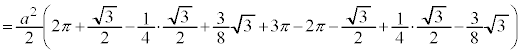
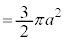
カージオイドCの周の長さ(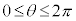 )を求めてみます。
)を求めてみます。
x軸から上の部分の周の長さの2倍と考えて、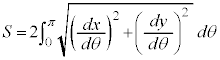
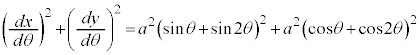
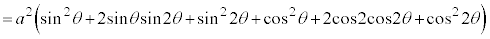
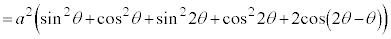
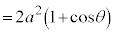
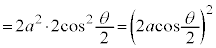
∴ 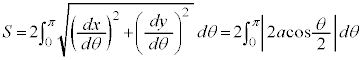
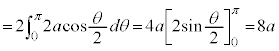
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 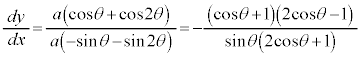 (媒介変数表示された関数の微分法を参照)
(媒介変数表示された関数の微分法を参照)