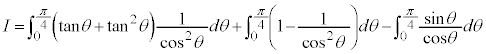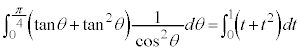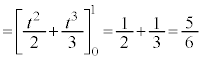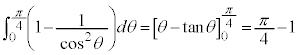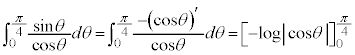置換積分 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
この項目では、不定積分の公式を参照してください。
また、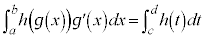
但し、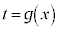 とおいた。
とおいた。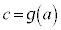 ,
,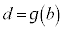 として、x:
として、x: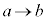 のとき、t:
のとき、t: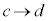 (
(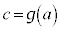 ,
,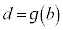 ),
),
また、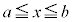 のとき、
のとき、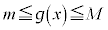 だとして、
だとして、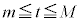 において
において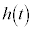 は連続,
は連続,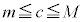 ,
,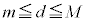 だとする。
だとする。
証明 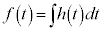 だとすると、
だとすると、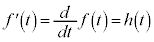
合成関数の微分法の公式より、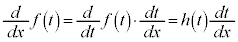
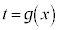 をxで微分すると、
をxで微分すると、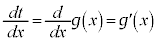
∴ 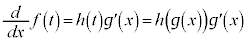
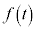 をxで微分すると、
をxで微分すると、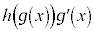 になる、ということは、
になる、ということは、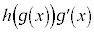 をxで積分すると
をxで積分すると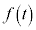 になるということです。
になるということです。
つまり、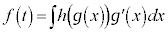 (
(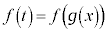 )
)
∴ 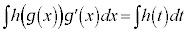
また、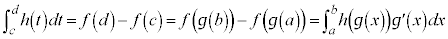 (証明終)
(証明終)
積分の計算は微分の計算と違って、必ずできるという保証がないのです。例えば、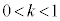 のとき、
のとき、
という形の積分は、指数関数や三角関数では表せないことが知られています。
ですが、そのままの形では積分の計算ができなくても、文字の置き換えを行うことにより、積分の計算が行える場合があります。
という形をしていて、計算のできない積分があった場合に、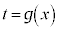 とおくと、
とおくと、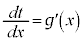
そこで、積分の中の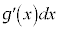 を
を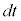 で置き換えて、xに関する積分をtに関する積分
で置き換えて、xに関する積分をtに関する積分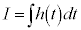 に直してしまうことができます。
に直してしまうことができます。
定積分の場合には、積分範囲の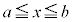 はxに関する範囲なので、tに間する積分に直す場合には、
はxに関する範囲なので、tに間する積分に直す場合には、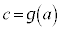 ,
,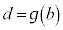 として、x:
として、x: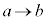 のとき、t:
のとき、t: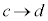 なので、
なので、
この形に直すと積分が計算できる場合があります。ただし、置換積分は、いつもうまくいくとは限らないことに注意してください。
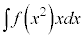 という形の積分は、
という形の積分は、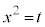 とおくと、うまくいくことがあります。
とおくと、うまくいくことがあります。
例1 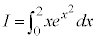
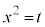 とおくと、
とおくと、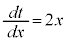 ∴
∴ 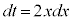
x::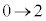 のとき、t:
のとき、t: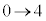
∴ 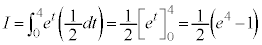
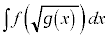 の場合には、
の場合には、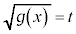 とおいて、xについて解いてから、
とおいて、xについて解いてから、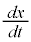 を求めます。
を求めます。
例2 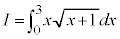
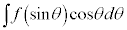 の場合には、
の場合には、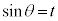 とおくと、
とおくと、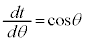 ∴
∴ 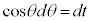
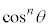 が被積分関数の中にあるときには、nが奇数になっているときに、
が被積分関数の中にあるときには、nが奇数になっているときに、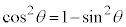 として、うまくいくときがあります。
として、うまくいくときがあります。
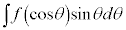 の場合には、
の場合には、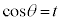 とおくと、
とおくと、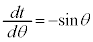 ∴
∴ 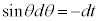
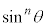 が被積分関数の中にあるときには、nが奇数になっているときに、
が被積分関数の中にあるときには、nが奇数になっているときに、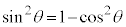 として、うまくいくときがあります。
として、うまくいくときがあります。
例3 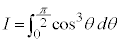
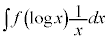 の場合には、
の場合には、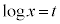 とおくと、うまくいくことがあります。
とおくと、うまくいくことがあります。
例4 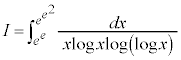
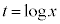 とおくと、
とおくと、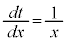 ,
,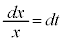 x:
x: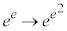 のとき、t:
のとき、t: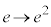
∴ 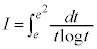 さらに、
さらに、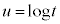 とおくと、
とおくと、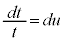 t:
t: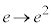 のとき、u:
のとき、u: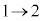
∴ 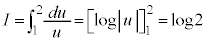
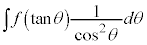 の場合には、
の場合には、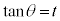 とおくと、うまくいくことがあります。
とおくと、うまくいくことがあります。
例5 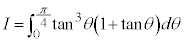
∴ 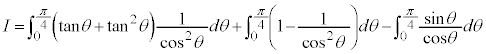 第1項の積分は、
第1項の積分は、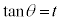 とおくと、
とおくと、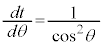 ∴
∴ 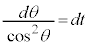 θ :
θ :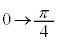 のとき、t:
のとき、t: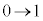 より、
より、 第2項の積分は、
第3項の積分は、
以上より、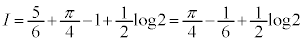
注意 上記の置換積分で、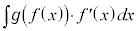 という形をしている積分では、文字の置き換えが面倒なので、
という形をしている積分では、文字の置き換えが面倒なので、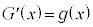 として、
として、
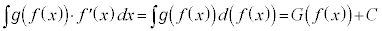 (C:積分定数)
(C:積分定数)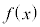 を固まりとして文字のように思って積分の計算をします。
を固まりとして文字のように思って積分の計算をします。
以下のように、定積分のときには、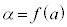 ,
,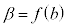 として、積分範囲を入れかえる必要がないので便利です。
として、積分範囲を入れかえる必要がないので便利です。
これを、高校の教科書風に計算を書くのであれば、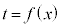 とおいて、
とおいて、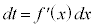 ,x:
,x: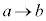 のとき、t:
のとき、t: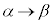 より、
より、
となります。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 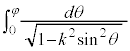
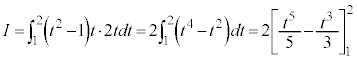
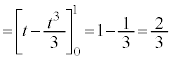
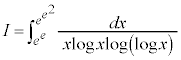
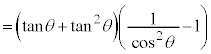 (∵
(∵