円と図形 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
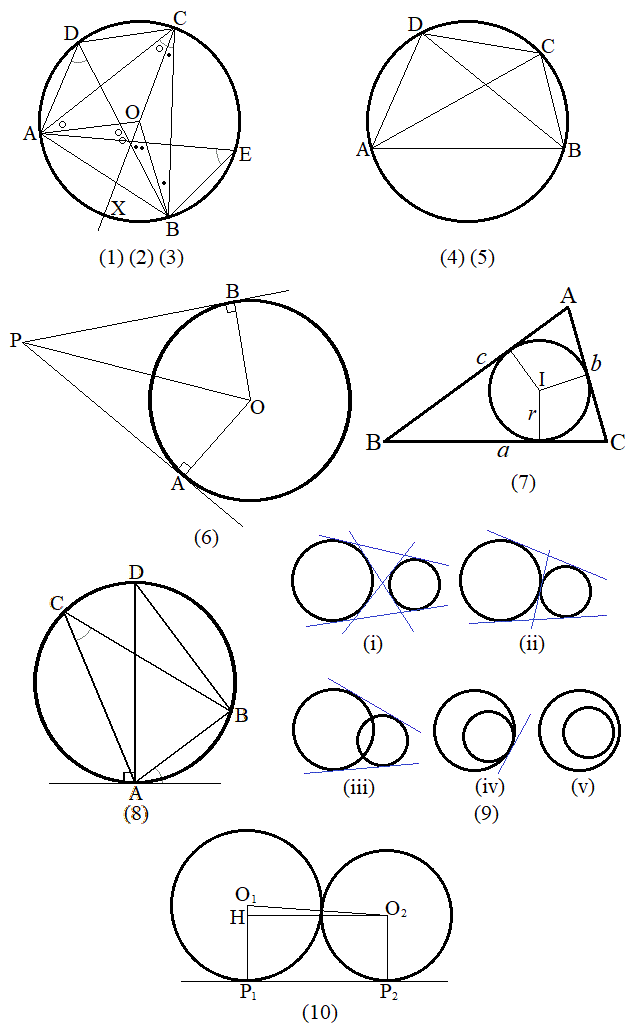 円周上の異なる2点を固定する。この2定点と円の中心を線分で結ぶとき、2線分のなす角を中心角と言う。この2定点とは異なる円周上の点をとって2定点と線分で結ぶとき、2線分のなす角を円周角と言う。
円周上の異なる2点を固定する。この2定点と円の中心を線分で結ぶとき、2線分のなす角を中心角と言う。この2定点とは異なる円周上の点をとって2定点と線分で結ぶとき、2線分のなす角を円周角と言う。
(1) 円周角の大きさは中心角の大きさの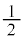 。
。
(2) 円周角の定理:円周上に異なる2点をとるとき、この2点を結ぶ弦(弧)の上に立つ円周角は等しい。
(3) 円周角の定理の逆:四角形ABCDについて、 であれば、この四角形は円に内接する。
であれば、この四角形は円に内接する。 (4) 定理:円に内接する四角形の対角は補角をなす。
(5) (3)の定理の逆:対角が互いに補角をなす四角形は円に内接する。
(6) 定理:円外の1点から円に引いた2接線の長さは等しい。
(7) 3辺の長さをa,b,cとする三角形の内接円の半径をrとすると、三角形の面積Sは、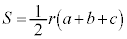
(8) 接弦角の定理:円周上の2点A,Bを結ぶ線分と、AまたはBにおける円の接線とがなす角は、弦AB(劣弧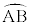 とします。なお、優弧でもABと接線のなす角を優角とすれば接弦角の定理が成り立ちます)の上に立つ円周角と等しい。
とします。なお、優弧でもABと接線のなす角を優角とすれば接弦角の定理が成り立ちます)の上に立つ円周角と等しい。 (9) 2円の共通接線の本数 (i) 2円に共通部分がない:4本 (ii) 2円が外接する:3本 (iii) 2円が2点で交わる:2本 (iv) 2円の一方が他方に内接する:1本 (v) 2円の一方が他方を含む:0本
(10) 2円の共通接線に関する技巧:2円の中心を結び、これを斜辺とする直角三角形を作る。
まず、(1)〜(8)の証明を書いておきます。
(1) 中心をOとする円周上に異なる3点A,B,Cをとります。線分COのO側への延長線と円との交点をXとします。
・A,O,Cが一直線上のとき(XとAが一致します。XとBが一致し、B,O,Cが一直線上のときも同様)、 より、△OBCは二等辺三角形です。よって、
より、△OBCは二等辺三角形です。よって、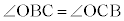 ,中心角
,中心角 は△OBCの外角で、
は△OBCの外角で、 ・XがAともBとも一致せず、A,O,Cも、B,O,Cも一直線上にない場合、△OBC,△OCAがともに存在します。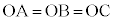 より、△OBC,△OCAはともに二等辺三角形です。よって、
より、△OBC,△OCAはともに二等辺三角形です。よって、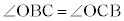 ,
,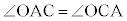
また、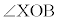 は△OBCの外角で、
は△OBCの外角で、 同様に、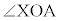 は△OACの外角で、
は△OACの外角で、 (i) CとXが直線ABの逆側にあるとき、 の場合には
の場合には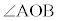 を優角(
を優角(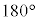 より大きい方の角)として、
より大きい方の角)として、 (ii) CとXがともに直線ABに関して同じ側にあるとき、円周上にA,B,X,Cの順に並ぶ場合(A,B,C,Xの順に並ぶ場合も同様です)には、
(2) 円周上に異なる2点A,Bをとり、この2点と異なる円周上の点C,Dを直線ABに関して同じ側にとると、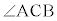 ,
,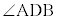 は、弦AB(弧
は、弦AB(弧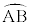 )の上に立つ円周角です。よって(1)により、
)の上に立つ円周角です。よって(1)により、 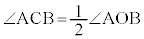 ,
,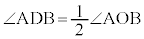
即ち、弦AB(弧 )の上に立つ円周角は等しくなります。
)の上に立つ円周角は等しくなります。
(3) Dが△ABCの外接円の周上の点ではないとして、外接円と直線ADとの交点のうちAでない方をEとします。円周角の定理(2)により、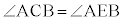 です。Dが線分AE上のE以外の点であれば、
です。Dが線分AE上のE以外の点であれば、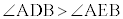 より条件に反します。Dが半直線AE上のEに関してAと反対側の点であれば、
より条件に反します。Dが半直線AE上のEに関してAと反対側の点であれば、 より条件に反します。よって、DはEに一致し、四角形ABCDは円に内接します。
より条件に反します。よって、DはEに一致し、四角形ABCDは円に内接します。
(4) 円周角の定理(2)により、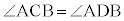 ,
,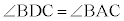
△ABCにおいて、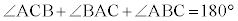
よって、 同様に、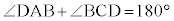 ,よって、円に内接する四角形の対角は補角をなします。
,よって、円に内接する四角形の対角は補角をなします。
(5) 四角形ABCDで対角が補角をなし、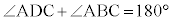 だとします。△ABCの外接円
だとします。△ABCの外接円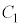 の円周上で直線ABに関してC,Dと同じ側に点Eをとると、四角形ABCEは円
の円周上で直線ABに関してC,Dと同じ側に点Eをとると、四角形ABCEは円 に内接します。(4)により、
に内接します。(4)により、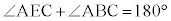
よって、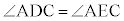 ,円周角の定理の逆(3)により、Dも円周
,円周角の定理の逆(3)により、Dも円周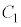 上の点であり、四角形ABCDは円
上の点であり、四角形ABCDは円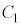 に内接します。
に内接します。
(6) Oを中心とする円に円外の点Pから接線を2本引き、接点をA,Bとします。△OAPと△OBPにおいて、 (円の半径),OP共通,
(円の半径),OP共通, より、△OAP ≡ △OBP ∴
より、△OAP ≡ △OBP ∴ 
即ち、円外の1点から円に引いた2接線の長さは等しくなります。
(7) 内接円の中心(内心です。三角形の五心を参照)をIとします。
(8) 円周上の点Aで(点Bにおける接線も同様)接線を引き、円周上にAと異なる点Dを、DAが接線と垂直になるようにとります。DAは円の直径なので、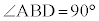 より、
より、 ですが、これは接線と弦ABのなす角です。円周上にA,Bとは異なる点Cをとると、円周角の定理(2)より、
ですが、これは接線と弦ABのなす角です。円周上にA,Bとは異なる点Cをとると、円周角の定理(2)より、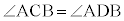
よって、弦の一端に引いた接線と弦のなす角は、この弦(劣弧)の上に立つ円周角と等しくなします。
(9) 2円の位置関係は、右上図の5通りあり、その各々について、図の青線のように接線を引くことができます。
(10) 2円が接するような状況を考える問題があります。このとき、一方の円(半径 )の中心
)の中心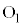 と接点
と接点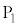 とを結ぶ直線に、もう一方の円(半径
とを結ぶ直線に、もう一方の円(半径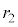 )の中心
)の中心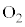 から垂線
から垂線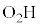 を下ろすと、直角三角形
を下ろすと、直角三角形 ができます。
ができます。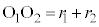 ,
,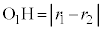 より、
より、 この事実を利用して解く問題があります。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。なお、解答は、
苦学楽学塾制作です。©2005-2026(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。