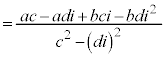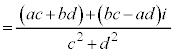複素数の計算 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
虚数単位iは、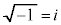 として定義されます。
として定義されます。
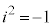 ですが、
ですが、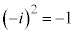 なので、iも
なので、iも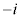 も
も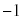 の平方根です。
の平方根です。
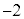 の平方根は、2次方程式:
の平方根は、2次方程式: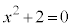 の2解になります。
の2解になります。
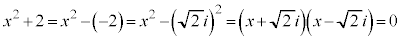 より、
より、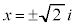
つまり、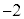 の平方根は、
の平方根は、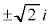 の2個あります。
の2個あります。
一般に、負数aの平方根は、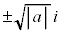 の2個あります。
の2個あります。
正数aの平方根では、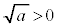 ですが、負数aの平方根では、
ですが、負数aの平方根では、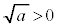 は言えません。負数の平方根は虚数なので、正負を考えることはできません。
は言えません。負数の平方根は虚数なので、正負を考えることはできません。
また、負数の平方根同士の積や商の計算には注意が必要です。
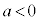 ,
,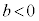 のとき、
のとき、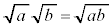 ,
,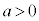 ,
,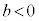 のとき、
のとき、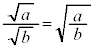 とはなりません。
とはなりません。
例えば、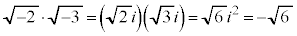 ,
,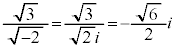 です。
です。
複素数zが、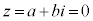 (a,bは実数)となるとき、
(a,bは実数)となるとき、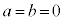 です。
です。
仮に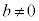 だとすると、
だとすると、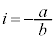 となり、虚数単位が実数という矛盾が起きるので、
となり、虚数単位が実数という矛盾が起きるので、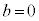 ,従って、
,従って、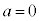 です。
です。
2つの複素数の間に相等しいという関係があるとき、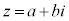 ,
,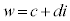 (a,b,c,dは実数)として、
(a,b,c,dは実数)として、
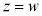 ,つまり、
,つまり、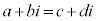 が成り立つとき、
が成り立つとき、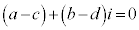
従って、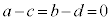 ,つまり、
,つまり、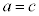 かつ
かつ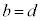 となります。
となります。
さらに言い換えると、2つの複素数が等しいと言うことは、2つの複素数の実部と虚部がともに等しいということです。
実数同士であれば、大小関係を考えることができますが、虚数同士、虚数と実数の間で大小関係を考えることはできません。
複素数同士の四則計算では、虚数単位iを文字として扱って計算を行い、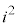 が出てきたら、
が出てきたら、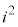 を
を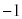 で置き換えます。
で置き換えます。
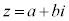 ,
,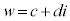 (a,b,c,dは実数)として、
(a,b,c,dは実数)として、
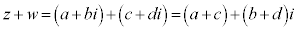
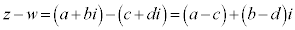
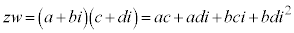
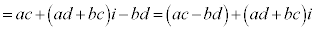
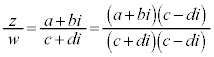 (この操作を分母の実数化と言います)
(この操作を分母の実数化と言います)
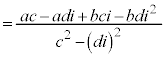
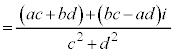
のように計算します。
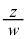 の計算途中に出てくる、
の計算途中に出てくる、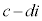 という形は複素数の計算でよく出てくる形です。
という形は複素数の計算でよく出てくる形です。
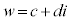 に対して、
に対して、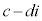 を
を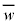 と書いて、wの共役複素数と言います(共役複素数を参照)。
と書いて、wの共役複素数と言います(共役複素数を参照)。
また、分母の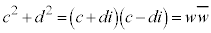 は0以上の実数ですが、
は0以上の実数ですが、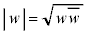 を複素数wの絶対値と言います。複素数
を複素数wの絶対値と言います。複素数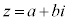 (a,bは実数)に対して、
(a,bは実数)に対して、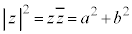 です。
です。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 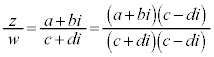 (この操作を分母の実数化と言います)
(この操作を分母の実数化と言います)