���f�������@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���f��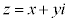 (x�Cy�͎����C
(x�Cy�͎����C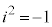 )��x�Cy�����W���ʏ�̓_P
)��x�Cy�����W���ʏ�̓_P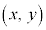 �ɑΉ�������Ƃ��A���̕��ʂ����f�������Ƃ����B���̓_��P
�ɑΉ�������Ƃ��A���̕��ʂ����f�������Ƃ����B���̓_��P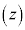 �ƕ\���A�hz�̕\���_P�h�Ƃ���������������B
�ƕ\���A�hz�̕\���_P�h�Ƃ���������������B
�ɁA���a
���f�����ʂł͍��W���ʂ�x���������Ay���������Ƃ����B���f���̎��������W���ʂ�x���W�ɑΉ����A���������W���ʂ�y���W�ɑΉ�����B
���f��z�����W���ʏ�̈ʒu�x�N�g��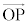 �Ɗ֘A�Â��邱�Ƃ��ł���B
�Ɗ֘A�Â��邱�Ƃ��ł���B
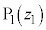 �C
�C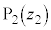 �C
�C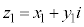 �C
�C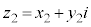 (
(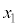 �C
�C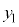 �C
�C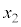 �C
�C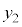 �͎���)�Ƃ��āA
�͎���)�Ƃ��āA
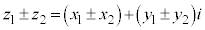 �̕\���_�̈ʒu�x�N�g����
�̕\���_�̈ʒu�x�N�g����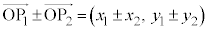
k�������Ƃ��āA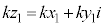 �̕\���_�̈ʒu�x�N�g����
�̕\���_�̈ʒu�x�N�g����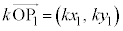
���f�����ʏ��2�_�Ԃ̋���
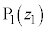 �C
�C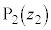 �C
�C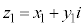 �C
�C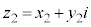 (
(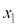 �C
�C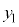 �C
�C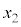 �C
�C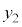 �͎���)�Ƃ��āA
�͎���)�Ƃ��āA
2�_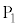 �C
�C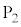 �̋����́A
�̋����́A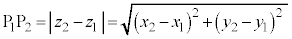 �ŗ^������B
�ŗ^������B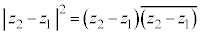 �ł��B
�ł��B
���f�����ʏ�̉~
C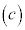 �Cr�𐳂̐��Ƃ��āA
�Cr�𐳂̐��Ƃ��āA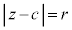 �����_P
�����_P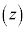 �́AP��C�̋��������lr������AC�𒆐S�Ƃ��锼�ar�̉~��`���B
�́AP��C�̋��������lr������AC�𒆐S�Ƃ��锼�ar�̉~��`���B
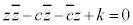 ����@ �Ƃ����`�̎�(
����@ �Ƃ����`�̎�(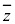 �Cz�̌W��c�C
�Cz�̌W��c�C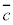 ���݂��ɋ����ł��邱�Ƃɒ���)���������ꍇ�A�܂�
���݂��ɋ����ł��邱�Ƃɒ���)���������ꍇ�A�܂�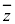 �ł�����B������o���Ă������ƁB
�ł�����B������o���Ă������ƁB
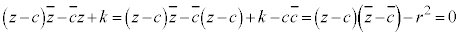 �C�������A
�C�������A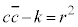 �Ƃ������B
�Ƃ������B
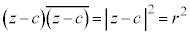 �@��
�@�� 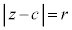 �ƂȂ�A���@��
�ƂȂ�A���@��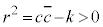 �̂Ƃ��ɂ́A�~��\���B
�̂Ƃ��ɂ́A�~��\���B
���f�����ʏ�̒���
A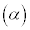 �CB
�CB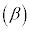 �Ƃ��āA
�Ƃ��āA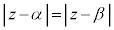 ���݂����_P
���݂����_P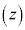 �́A
�́A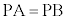 ������A����AB�̐���������`���B���ӂ�2�悵�āA
������A����AB�̐���������`���B���ӂ�2�悵�āA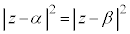 �C
�C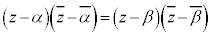
�� 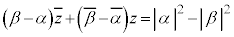
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B