�]���藝�@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
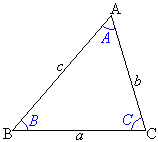 ��1�]���藝
��1�]���藝
�E�}�� �ɂ����āA
�ɂ����āA
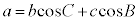
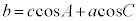
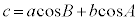
[�ؖ�]�@���_A����Ε�BC�ɉ��낵�������̑���H�Ƃ��܂��B
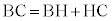 �C
�C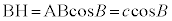 �C
�C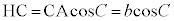 ���A
���A
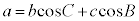
���l�ɁA���_B����Ε�CA�ɐ��������낷���Ƃɂ��A
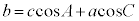
���_C����Ε�AB�ɐ��������낷���Ƃɂ��A
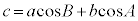
(�ؖ��I)
(�O�p���A�O�p��̊g�����Q��)
 ��2�]���藝
��2�]���藝
�E�}��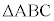 �ɂ����āA
�ɂ����āA
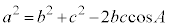
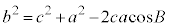
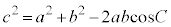
��2�]���藝��������u�]���藝�v�ł��B
[�ؖ�]�@��1�]���藝���A
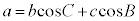 ����@
����@
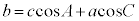 ����A
����A
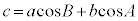 ����B
����B
�A���A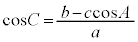 �C�B���A
�C�B���A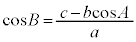
�@�ɑ������ƁA
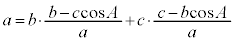
������Đ�������ƁA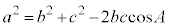
���l�ɂ��āA�@�C�B�œ���ꂽ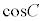 �C
�C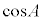 ���A�ɑ�����邱�Ƃɂ��A
���A�ɑ�����邱�Ƃɂ��A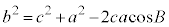
�@�C�A�œ���ꂽ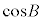 �C
�C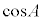 ���B�ɑ�����邱�Ƃɂ��A
���B�ɑ�����邱�Ƃɂ��A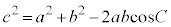
(�ؖ��I)
�]���藝�ɂ����āAA�CB�CC�̂����ꂩ�����p�ł���A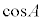 �C
�C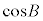 �C
�C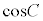 �̂����ꂩ���[���ł���A�O�����̒藝�ɂȂ�܂��B
�̂����ꂩ���[���ł���A�O�����̒藝�ɂȂ�܂��B
�]���藝��ό`����ƁA3�ӂ̒�������A�O�p�`�̓��p�̗]�������߂�����������܂��B
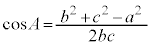 �C
�C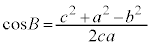 �C
�C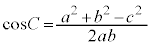
��D3�ӂ��A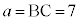 �C
�C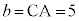 �C
�C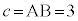 �ł���O�p�`�̒��pA�̑傫�������߂܂��B
�ł���O�p�`�̒��pA�̑傫�������߂܂��B
�]���藝���A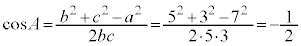
����āA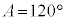 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B