センター数学IA '09年第2問
aを定数とし、xの2次関数
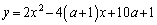･･･①
グラフGの頂点の座標をaを用いて表すと
である。
(1) グラフGがx軸と接するのは
のときである。
(2) 関数①の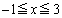
における最小値をmとする。 となるのは
のときである。また
である。
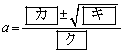
したがって、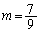
となるのは のときである。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 2次関数の基本問題です。場合分け以降は、やや面倒です。
①を平方完成すると、
これより頂点の座標は、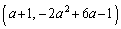
(ア) 1 (イ) － (ウ) 2 (エ) 6 (オ) 1 ......[答]
(1) グラフGがx軸と接するのは、頂点のy座標が0のときです。
∴ 
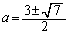
(カ) 3 (キ) 7 (ク) 2 ......[答]
(2) 関数①の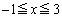
における最小値mを求めるために、頂点のx座標
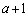が、この範囲の右側にあるのか、範囲に含まれるのか、範囲の左側にくるのか、で、場合分けします(2次関数の最大・最小を参照)。つまり、
，
，
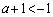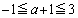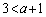，従って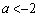、(i) 
，(ii)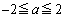 
，(iii) 
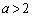と場合わけします。 
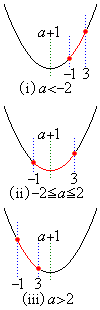(i) 
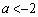のとき、右図より、関数①は
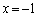のときに最小値をとります。とすると、
となりますが、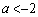
を満たさないので不適です。 (ii)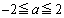 
のとき、右図より、関数①は
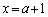のときに最小値をとります。 とすると、整理して、
(iii)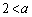 
のとき、右図より、関数①は
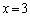のときに最小値をとります。 とすると、
(
)
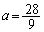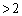【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
のとき 
のとき 
より、
となるのは、
のとき。
のとき、
のとき、
となるのは、
のとき。