2次関数 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
標準形: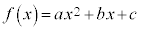
2次式で表される関数が2次関数です。
 座標平面上で2次関数のグラフは放物線になります。
座標平面上で2次関数のグラフは放物線になります。
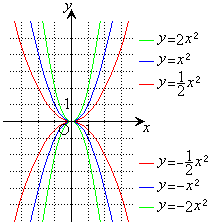
2次関数: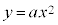 ・・・① のグラフを
・・・① のグラフを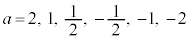 について描いたものを右図に示します。
について描いたものを右図に示します。
右図の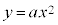 のグラフは、いずれもy軸に関して対称になります。なぜなら、
のグラフは、いずれもy軸に関して対称になります。なぜなら、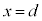 ,
,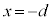 に対するyの値はともに
に対するyの値はともに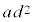 で等しいからです。
で等しいからです。
この対称軸のことを放物線の軸と言います。
軸と放物線との交点を放物線の頂点と言います。
右図の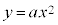 のグラフの頂点は、いずれも原点O
のグラフの頂点は、いずれも原点O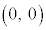 です。軸はy軸です。
です。軸はy軸です。
これによると、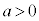 のときは、
のときは、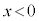 のとき(軸の左側)には関数値は減少、
のとき(軸の左側)には関数値は減少、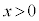 のとき(軸の右側)には関数値は増加します。
のとき(軸の右側)には関数値は増加します。
このとき、グラフが下に向かってふくらんでいるので、下に凸と言います。
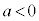 のときは、
のときは、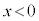 のとき(軸の左側)には関数値は増加、
のとき(軸の左側)には関数値は増加、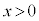 のとき(軸の右側)には関数値は減少します。
のとき(軸の右側)には関数値は減少します。
このとき、グラフは上に向かってふくらんでいるので、上に凸と言います。
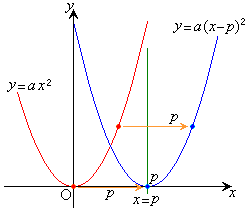 ①のxを
①のxを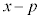 に置き換えた2次関数:
に置き換えた2次関数: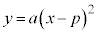 ・・・② のグラフを考えてみます。
・・・② のグラフを考えてみます。
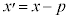 とおくと、②は
とおくと、②は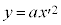 となりますが、このグラフはy軸を軸とし、原点を頂点とする放物線になります。
となりますが、このグラフはy軸を軸とし、原点を頂点とする放物線になります。
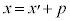 なので、
なので、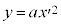 のグラフ上の点は、②ではx座標がpだけ加えられた点に来ます。
のグラフ上の点は、②ではx座標がpだけ加えられた点に来ます。
これは、右図のようにpだけx軸方向に平行移動した点にくることを意味しています。
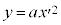 のグラフ上の点全てについてこれが言えるので、②のグラフは、y軸を軸とし、原点を頂点とする放物線をx軸方向にpだけ平行移動したグラフになります。
のグラフ上の点全てについてこれが言えるので、②のグラフは、y軸を軸とし、原点を頂点とする放物線をx軸方向にpだけ平行移動したグラフになります。
②のグラフでは、軸はy軸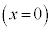 をx軸方向にpだけ平行移動した直線
をx軸方向にpだけ平行移動した直線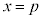 となり、頂点は原点O
となり、頂点は原点O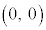 をx軸方向にpだけ平行移動した点
をx軸方向にpだけ平行移動した点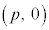 となります。
となります。
つまり、②のグラフは、直線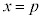 を軸とし、
を軸とし、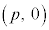 を頂点とする放物線になります。
を頂点とする放物線になります。
2次関数: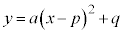 ・・・③ のグラフを考えてみます。
・・・③ のグラフを考えてみます。
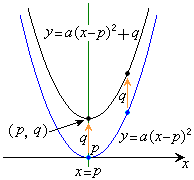 ②のグラフと比べると、y座標がどのxの値に対してもqずつ増えているので、右図のように、③のグラフは、②のグラフをy軸方向にqだけ平行移動したグラフになります。
②のグラフと比べると、y座標がどのxの値に対してもqずつ増えているので、右図のように、③のグラフは、②のグラフをy軸方向にqだけ平行移動したグラフになります。
軸は直線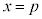 のままですが、頂点は、②のグラフの頂点
のままですが、頂点は、②のグラフの頂点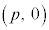 からy軸方向にqだけ平行移動した点
からy軸方向にqだけ平行移動した点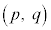 に移ります。
に移ります。
つまり、③のグラフは、直線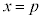 を軸とし、
を軸とし、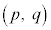 を頂点とする放物線になります。
を頂点とする放物線になります。
一般的な場合で、2次関数: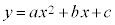 ・・・④ のグラフを考察してみます。標準形を平方完成すると、
・・・④ のグラフを考察してみます。標準形を平方完成すると、
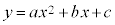
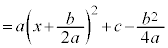 ・・・⑤
・・・⑤
となります。
これは、③において、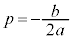 ,
,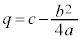 としたものです。
としたものです。
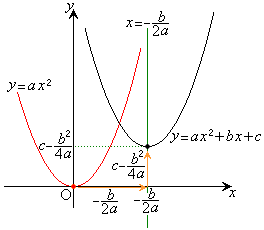 つまり、④のグラフは、直線
つまり、④のグラフは、直線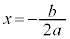 を軸とし、
を軸とし、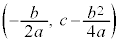 を頂点とする放物線になります。
を頂点とする放物線になります。
頂点のy座標は、④で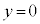 としてできる2次方程式:
としてできる2次方程式: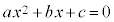 の判別式:
の判別式: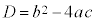 を用いて、
を用いて、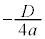 と表されることに注意してください。
と表されることに注意してください。
④のグラフは、①のグラフをx軸方向に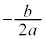 ,y軸方向に
,y軸方向に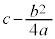 だけ平行移動したグラフだと言うこともできます。
だけ平行移動したグラフだと言うこともできます。
従って、①の頂点も原点Oからx軸方向に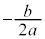 ,y軸方向に
,y軸方向に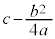 だけ平行移動されることになります。
だけ平行移動されることになります。
例.2次関数: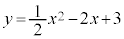 のグラフ
のグラフ
右辺を平方完成すると、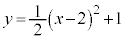
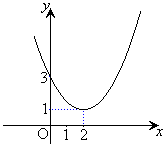 このグラフはy軸を軸、原点を頂点とする下に凸な放物線
このグラフはy軸を軸、原点を頂点とする下に凸な放物線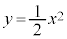 を、x軸方向に2,y軸方向に1だけ平行移動して得られる放物線です。
を、x軸方向に2,y軸方向に1だけ平行移動して得られる放物線です。
グラフは右図。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。