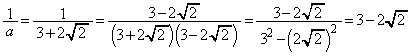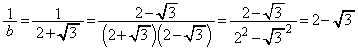センター数学IA '11年第1問
[1] 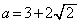 ,
,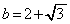 とすると
とすると
である。このとき、不等式
を満たすxの値の範囲は
となる。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 分母の有理化の問題です。後半の計算に前半の計算結果を活かすようにしましょう。
(ア) 3 (イ) 2 (ウ) 2 ......[答]
(エ) 2 (オ) 3 ......[答]
(カ) 8 (キ) 2 (ク) 6 (ケ) 3 ......[答]
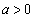 ,
,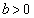 なので、
なので、
∴ 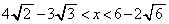
(コ) 4 (サ) 2 (シ) 3 (ス) 3 (セ) 6 (ソ) 2 (タ) 6 ......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
[2] 実数a,bに関する条件p,qを次のように定める。
(1) 次の ~
~ のうち、命題「q ⇒ p」に対する反例になっているのは
のうち、命題「q ⇒ p」に対する反例になっているのは である。
である。 (2) 命題「p ⇒ q」の対偶は「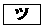 ⇒
⇒  」である。
」である。  ,
, に当てはまるものを、次の
に当てはまるものを、次の ~
~ のうちから一つずつ選べ。
のうちから一つずつ選べ。
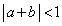 かつ
かつ 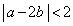

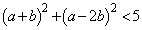

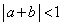 または
または 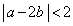

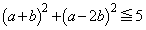

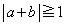 かつ
かつ 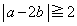

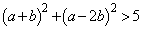

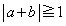 または
または 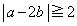

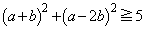
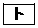 。
。
 に当てはまるものを、次の
に当てはまるものを、次の ~
~ のうちから一つ選べ。
のうちから一つ選べ。 必要十分条件である
必要十分条件である 必要条件であるが、十分条件ではない
必要条件であるが、十分条件ではない 十分条件であるが、必要条件ではない
十分条件であるが、必要条件ではない 必要条件でも十分条件でもない
必要条件でも十分条件でもない
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 まともに体当たりしなくてもよいでしょう。(1)は、暗に、適当に値を代入して、真偽や、必要条件か、十分条件かを判断してはどうか、ということを示唆しています。
ですが、アインシュタインの理論が正しいか誤っているかをカンで判断してよい、と言うのであれば、「論理」の問題を出題する意味があるのでしょうか?
(1) 命題「q ⇒ p」に対する反例というのは、条件qを満たすが条件pは満たさない例、となるものです。 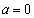 ,
,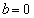 のとき、
のとき、条件pは、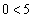 となり成立。条件qは、
となり成立。条件qは、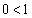 または
または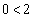 となり成立。よって、反例にはなりません。
となり成立。よって、反例にはなりません。 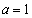 ,
,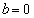 のとき、
のとき、条件pは、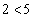 となり成立。条件qは、
となり成立。条件qは、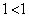 または
または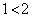 となり成立。よって、反例にはなりません。
となり成立。よって、反例にはなりません。 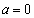 ,
,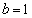 のとき、
のとき、条件pは、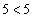 となり不成立。条件qは、
となり不成立。条件qは、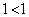 または
または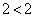 となり不成立。よって、反例になりません。
となり不成立。よって、反例になりません。 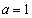 ,
,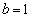 のとき、
のとき、条件pは、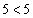 となり不成立。条件qは、
となり不成立。条件qは、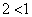 または
または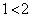 となり成立。よって、これが反例になります。
となり成立。よって、これが反例になります。 (チ)  ......[答]反例が挙げられるので、命題「q ⇒ p」は偽です。 ・・・①
......[答]反例が挙げられるので、命題「q ⇒ p」は偽です。 ・・・① (2) 命題「p ⇒ q」の対偶は、「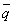 ⇒
⇒ 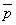 」です。
」です。 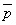 は、
は、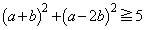
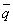 は、
は、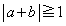 かつ
かつ 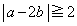
(ツ)  (テ)
(テ)  ......[答]
......[答]というわけで、対偶が成り立つので、元の命題「p ⇒ q」は真です。 ・・・②
(3) ①,②より、pはqであるための十分条件ですが、必要条件ではありません。
(ト)  ......[答]
......[答] 追記.落ち着いてやれば以上の通りで、出題者の意図もそこにあります。ですが、センター試験には厳しい時間制限があって最終解答しか要求されません。条件qの「または」という言葉と、a,bの絶対値が大きくても条件qが成立する場合があることから、カンでマークしておけば得点できるでしょう。例年の問題も証明してみる必要のない問題です。
数学TOP TOPページに戻る
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。