センター数学IA '12年第1問
[1](1) 不等式 の解は
の解は である。
である。 以下、aを自然数とする。
(2) 不等式
 ・・・①
・・・①の解は である。
である。 (3) 不等式①を満たす整数xの個数をNとする。 のとき、
のとき、 である。また、aが4,5,6,・・・と増加するとき、Nが初めて
である。また、aが4,5,6,・・・と増加するとき、Nが初めて より大きくなるのは、
より大きくなるのは、 のときである。
のときである。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 不等式を満たす整数解の個数の問題です。なお、1次方程式・1次不等式を参照してください。
(1) 
(ア) - (イ) 2 (ウ) 1 ......[答]
(2)  ・・・①
・・・① (エ) 1 (オ) 2 ......[答]
(3)  のとき、
のとき、 を満たす整数xは、
を満たす整数xは、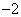 ,
, ,0,1の4個で、
,0,1の4個で、
(カ) 4 ......[答]②は、 のとき、
のとき、 ,これを満たす整数xは、
,これを満たす整数xは、 ,
,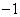 ,0,1の4個で、
,0,1の4個で、
②は、 のとき、
のとき、 ,これを満たす整数xは、
,これを満たす整数xは、 ,
, ,
, ,0,1,2の6個で、
,0,1,2の6個で、 Nが初めて4より大きくなるのは、
Nが初めて4より大きくなるのは、 のときです。(キ) 5 ......[答]
のときです。(キ) 5 ......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
[2] kを定数とする。自然数m,nに関する条件p,q,rを次のように定める。
(1) 次の に当てはまるものを、下の
に当てはまるものを、下の ~
~ のうちから一つ選べ。
のうちから一つ選べ。 (2) 次の ~
~ に当てはまるものを、下の
に当てはまるものを、下の ~
~ のうちから一つずつ選べ。ただし、同じものを繰り返し選んでもよい。
のうちから一つずつ選べ。ただし、同じものを繰り返し選んでもよい。 (i)  とする。
とする。 pはqであるための 。
。 (ii)  とする。
とする。 pはrであるための 。pはqであるための
。pはqであるための 。
。  必要十分条件である
必要十分条件である
 必要条件であるが、十分条件でない
必要条件であるが、十分条件でない
 十分条件であるが、必要条件でない
十分条件であるが、必要条件でない
 必要条件でも十分条件でもない
必要条件でも十分条件でもない
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 相手の条件に対して「広い」方が必要条件、「狭い」方が十分条件、と、機械的に判断させないように、自然数、という指定をつけていますが、xy平面上で格子点を取ってみれば「広い」「狭い」で判断することができます。なお、条件と命題を参照してください。
(ク) 2 ......[答]
(2)(i)  のとき、p:
のとき、p: または
または ,q:
,q: となりますが、pを満たす整数の組
となりますが、pを満たす整数の組 の集合
の集合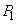 は、
は、 qを満たす整数の組 の集合もこれに一致します。従って、pはqであるための必要十分条件です。(ケ)
の集合もこれに一致します。従って、pはqであるための必要十分条件です。(ケ)  ......[答]
......[答] (ii)  のとき、
のとき、 rを満たす整数の組 の集合を
の集合を とすると、
とすると、 pを満たす整数の組 の集合を
の集合を とすると、
とすると、  ,
,
qを満たす整数の組 の集合を
の集合を とすると、
とすると、 よって、
即ち、q ⇒ p ⇒ r
pはrであるための十分条件であるが必要条件ではなく、pはqであるための必要条件であるが十分条件ではない、ということになります。(コ)  (サ)
(サ)  ......[答]
......[答]
数学TOP TOPページに戻る
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。  である。
である。