センター数学IA '12年第2問
[2] a，bを定数として2次関数
･･･①
である。以下、この頂点が直線
上にあるとする。このとき、
である。
(1) グラフGがx軸と異なる2点で交わるようなaの値の範囲は
である。また、Gがx軸の正の部分と負の部分の両方で交わるようなaの値の範囲は
である。
(2) 関数①の
における最小値が
となるのは 
または 
のときである。また、
のとき、関数①の
における最大値は
である。
一方、
のときの①のグラフをx軸方向に
，y軸方向に
だけ平行移動すると、
のときのグラフと一致する。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 2次関数の最大最小・グラフの平行移動に関する問題です。
･･･①
･･･②
(ア) 2 (イ) 4 (ウ) 4 ......[答]
この頂点が、
上にあるとき、
･･･③
(1) グラフGがx軸と異なる2点で交わるとき、Gは上に凸な放物線なので頂点のy座標は正です。
③より、
∴ 
(キ) － (ク) 9 (ケ) 4 ......[答]
Gがx軸の正の部分と負の部分の両方で交わるとき、Gのグラフはy軸と
の部分で交わります。①で
とすると、
，よって、③より、 
の解は、
より、(コ) 4 (サ) 3 ......[答]
(2) Gのグラフの軸の位置
が、
の範囲の中央(
)から左側か右側かで場合分けします。軸が範囲の中央から左にあるとき、
，つまり、
のとき、関数①は、範囲の右端
において最小で、③より、 ∴ 
(
)軸が範囲の中央から右にあるとき、つまり、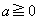
のとき、関数①は、範囲の左端
において最小で、③より、 ∴ 
(
)
(シ) － (ス) 3 (セ) 1 ......[答]
のとき、
なので、②より関数①は、 となり、Gの頂点は
で、
のとき、最大値
をとります。(ソ) － (タ) 1 (チ) 3 ......[答]
のとき、②より
なので、②より関数①は、 となり、Gの頂点は
に来ます。x軸方向に4，y軸方向に
平行移動すると頂点は
に来るので、
のときのグラフと一致します。(ツ) 4 (テ) － (ト) 1 (ナ) 6 ......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
