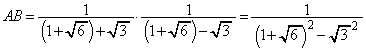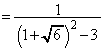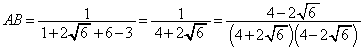センター数学IA '13年第1問
[1] 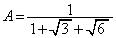 ,
,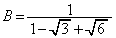 とする。
とする。
[2] 三角形に関する条件p,q,rを次のように定める。
p:三つの内角がすべて異なる。q:直角三角形でないr: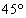 の内角は一つもない
の内角は一つもない 条件pの否定を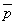 で表し、同様に
で表し、同様に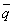 ,
,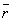 はそれぞれ条件q,rの否定を表すものとする。
はそれぞれ条件q,rの否定を表すものとする。 (1) 命題「r ⇒ (p または q)」の対偶は「 ⇒
⇒ 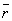 」である。
」である。  に当てはまるものを、次の
に当てはまるものを、次の 〜
〜 のうちから一つ選べ。
のうちから一つ選べ。
 (p かつ q)
(p かつ q)  (
(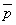 かつ
かつ 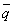 )
) (
(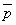 または q)
または q)  (
(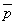 または
または 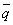 )
)(2) 次の 〜
〜 のうち、命題「(p または q) ⇒ r」に対する反例となっている三角形は
のうち、命題「(p または q) ⇒ r」に対する反例となっている三角形は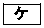 と
と である。
である。  と
と に当てはまるものを、
に当てはまるものを、 〜
〜 のうちから一つずつ選べ。ただし、
のうちから一つずつ選べ。ただし、 と
と の解答の順序は問わない。
の解答の順序は問わない。
 直角二等辺三角形
直角二等辺三角形
 内角が
内角が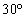 ,
,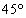 ,
,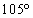 の三角形
の三角形
 正三角形
正三角形
 三辺の長さが3,4,5の三角形
三辺の長さが3,4,5の三角形
 頂角が
頂角が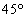 の二等辺三角形
の二等辺三角形(3) rは(p または q)であるための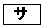 。
。  に当てはまるものを、次の
に当てはまるものを、次の 〜
〜 のうちから一つ選べ。
のうちから一つ選べ。
 必要十分条件である
必要十分条件である
 必要条件であるが、十分条件ではない
必要条件であるが、十分条件ではない
 十分条件であるが、必要条件ではない
十分条件であるが、必要条件ではない
 必要条件でも十分条件でもない
必要条件でも十分条件でもない
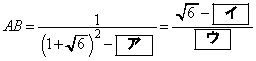
[1] 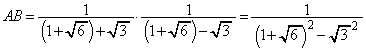
(ア) 3 ......[答]
(イ) 2 (ウ) 4 ......[答]
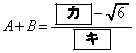
(エ) 2 (オ) 2 ......[答]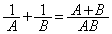 より、
より、 (カ) 4 (キ) 2 ......[答]
[2](1) 命題「r ⇒ (p または q)」の対偶は、「(p または 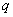 )でない ⇒ rでない」
)でない ⇒ rでない」 つまり、「(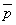 かつ
かつ 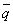 ) ⇒
) ⇒ 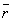 」(ク)
」(ク)  ......[答]
......[答] (2)  の内角が
の内角が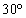 ,
,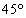 ,
,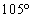 の三角形は、三つの内角がすべて異なり、また、直角三角形でもないので、「pまたはq」を満たしますが、
の三角形は、三つの内角がすべて異なり、また、直角三角形でもないので、「pまたはq」を満たしますが、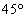 の内角があるので、rを満たしません。
の内角があるので、rを満たしません。  の頂角
の頂角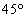 の二等辺三角形は、2つの底角が
の二等辺三角形は、2つの底角が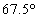 で直角三角形ではないので、「pまたはq」を満たしますが、
で直角三角形ではないので、「pまたはq」を満たしますが、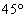 の内角があるので、rを満たしません。
の内角があるので、rを満たしません。
 と
と が「(pまたはq) ⇒ r」の反例です。
が「(pまたはq) ⇒ r」の反例です。 ,
, ,
, は、いずれも、「pまたはq」を満たしません。(ケ)
は、いずれも、「pまたはq」を満たしません。(ケ)  (コ)
(コ)  ......[答]
......[答](3) 命題「(p または q) ⇒ r」は、(2)のように、反例が存在するので偽です。
命題「r ⇒ (p または q)」の対偶は、(1)のように、「(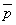 かつ
かつ 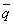 ) ⇒
) ⇒ 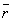 」
」
となりますが、「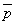 かつ
かつ 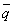 」という条件は、三つの内角のうちに同じ角があって、かつ、
」という条件は、三つの内角のうちに同じ角があって、かつ、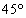 という内角を含む、という条件になりますが、このときは、
という内角を含む、という条件になりますが、このときは、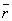 が成り立ちます。つまり、命題「r ⇒ (p または q)」は真です。
が成り立ちます。つまり、命題「r ⇒ (p または q)」は真です。
従って、rは(p または q)であるための十分条件ですが必要条件ではありません。(サ)  ......[答]
......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。