証明の技巧 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
命題P：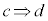
に対して、
命題：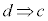
を命題Pの逆と言う。
命題：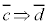
を命題Pの裏と言う。
命題：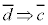
の対偶と言う。
例1．命題：“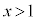
” ⇒ “
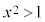”は真ですが、この命題の逆である命題：“
” ⇒ “
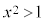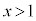”は偽です。
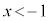となるxは、
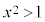は満たしますが、
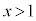は満たしません。
例1のように、ある命題：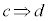
が真であっても、逆：
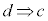も真であるとは限りません。
条件cを満たすものの集合をC，条件dを満たすものの集合をDとして、命題：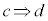
が真であるとき
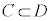ですが、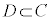
だとは限りません。
条件cが満たされていて、条件dが満たされないようなものがあるとき、つまり、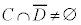
のときには、集合
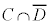の要素(右図×点)が、逆：
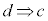が偽であることの反例になります。
命題：
を証明する場合には、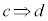
を示しただけでは証明したことになりません。逆：
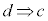も示してはじめて証明したことになります。
例2．実数x，yに対して、“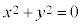
” ⇔ “
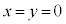”を証明します。
[証明]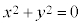 
であるとき、
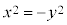･･･(＊) ですが、x，yが実数のとき、
，
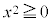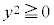より、(＊)の左辺
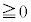かつ(＊)の右辺
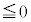であって、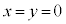
に限られます。
逆に、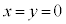
のとき、
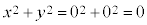(証明終)
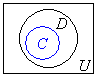全体集合をUとします。条件cを満たすものの集合をC，条件dを満たすものの集合をDとして、命題P：
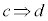が真であるとき
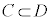です。このとき、右図より、
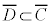です。ということは、命題：
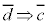(Pの対偶)が真だと言うことです。つまり、
“ ” ⇔ “ ” |
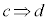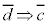命題そのものが証明しづらいときに、その命題の対偶を証明するという方法もあります(対偶参照)。
例3．“正の整数nについて、nを5で割った余りが2か3” ⇒ “nは平方数ではない”という命題を証明したいとします。
このままの形で証明しようとすると、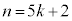
または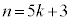
とおいて証明を始めることになりますが、簡単にはいきません。
もとの命題の対偶は、“nが平方数” ⇒ “正の整数nについて、nを5で割った余りは0か1か4”です。
これだと、0以上の整数kと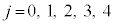
を用いて、
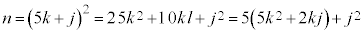とおくと、
nを5で割った余りは、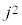
を5で割った余りに一致します。
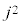を5で割った余りは、
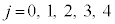に応じて、0，1，4，4，1となるので結論が示せました。
対偶を証明することにより、“正の整数nについて、nを5で割った余りが2か3” ⇒ “nは平方数ではない”という命題を証明したことになります。
「“.......ではない” ⇒ “........ ではない”」という形の命題の証明を考える場合には、対偶を考えるほうが良い場合があります。
“
” ⇔ “
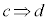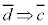”を利用した証明法がもう一つあります。
“
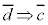”において、証明すべき結論dを否定すると
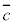になるということは、もとの条件cと矛盾が生ずると言うことです。
従って、証明すべき結論を否定して、与えられた条件と矛盾するということが導ければ、もとの命題を証明したことになります。
この証明法を背理法と言います。
例4．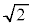
が無理数であることを背理法で証明します。
[証明]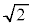 
が有理数だとして、互いに素な自然数p，qを用いて、
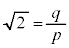とおけたとします。
分母を払って2乗すると、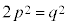
これはqが2の倍数であることを意味します。自然数kを用いて、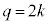
とおくと、
∴ 
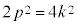
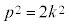
これはpが2の倍数であることを意味しますが、p，qが互いに素であることと矛盾します。
ということは、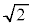
を既約分数に形に表すことはできないことを意味します。
よって、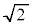
は無理数です。 (証明終)
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。