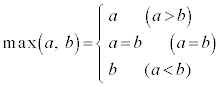�����@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�w��܂���1�C2�C3�C����C�Ɛ������鐔�����R���ƌ����܂��B
2�̎��R��n�Cm ( )�������Ă����Ƃ��A
)�������Ă����Ƃ��A �͎��R���ɂȂ�܂���B
�͎��R���ɂȂ�܂���B
 �̂Ƃ��A
�̂Ƃ��A
 �̂Ƃ��A
�̂Ƃ��A �͎��R���ł����A
�͎��R���ł����A ��k���g���āA
��k���g���āA �Ə����Ɩ���Ă��܂��B���R��k�����̐����A
�Ə����Ɩ���Ă��܂��B���R��k�����̐����A �����̐����ƌĂԂƖ��܂��B
�����̐����ƌĂԂƖ��܂��B
���̐����C0�C���̐��������킹�āA�P�������ƌĂт܂��B
�����́A�a�{�A���|�A�ρ~�ɂ��ĕ��Ă��܂��B
�܂�A2�̐���n�Cm�������Ă���ƁA �C
�C �C
�C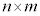 �̂�������܂������ɂȂ�Ƃ��������������Ă��܂��B
�̂�������܂������ɂȂ�Ƃ��������������Ă��܂��B
�ł����A�����ɂ��ẮA���Ă��܂���B �͐����ɂȂ�Ƃ͌���܂���B
�͐����ɂȂ�Ƃ͌���܂���B
����k�������āA �Ə�����Ƃ��A�܂�A
�Ə�����Ƃ��A�܂�A �ƂȂ�Ƃ��A�hn��m�Ŋ������h�ƌ����܂��B
�ƂȂ�Ƃ��A�hn��m�Ŋ������h�ƌ����܂��B
���̂Ƃ��An��m���{���ƌ����Am��n�����ƌ����܂��B
�S�Ă̐�����1�̔{���ł���A1�͑S�Ă̎��R���̖ł��B
2�̔{���������A2�̔{���łȂ���������ƌ����܂��B2�̔{����1�̈ʂ̐����������ł��B
�S�Ă̐����ɂ��āA0���������0�ɂȂ�̂ŁA0�͑S�Ă̐����̔{���ł��B
���R��n��10�i�@�ŕ\�����Ƃ��A �Ƃ��āA�e���̐���(
�Ƃ��āA�e���̐���( �C
�C �C
�C �C����C
�C����C �͐����A
�͐����A �C
�C �C
�C �C����C
�C����C )�̘a
)�̘a �Ƃ��܂��B
�Ƃ��܂��B
�EN��3�̔{�� �� n��3�̔{��
�EN��9�̔{�� �� n��9�̔{��
�En�̉�2����4�̔{�� �� n��4�̔{��
�En��1�̈ʂ̐�����0��5 �� n��5�̔{��
����n���A����m�Ck�Cr (�������A �Ƃ��܂�)��p���āA
�Ƃ��܂�)��p���āA
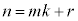 ����@
����@
�Ə�����Ƃ��A
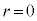 �̂Ƃ��ɂ́An��m�Ŋ����܂����A
�̂Ƃ��ɂ́An��m�Ŋ����܂����A
 �̂Ƃ��ɂ́An��m�Ŋ����܂���B���̂Ƃ���r��]��ƌ����܂��B
�̂Ƃ��ɂ́An��m�Ŋ����܂���B���̂Ƃ���r��]��ƌ����܂��B
�@���́A�����̖��ł悭�g���鎮�ł��B �Ƃ�����ɂ����Ɏv���o����悤�ɂ��Ă����܂��傤�B
�Ƃ�����ɂ����Ɏv���o����悤�ɂ��Ă����܂��傤�B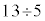 �͏���2�C�]�肪3�ł��B
�͏���2�C�]�肪3�ł��B
�藝�@�C�ӂ̐���n�ƁA���R��m�ɂ��āA (
( )��������k�Cr�͂���1�ʂ�Ɍ��܂�(������A�uk�Cr����ӓI�v�ƌ����܂�)�B
)��������k�Cr�͂���1�ʂ�Ɍ��܂�(������A�uk�Cr����ӓI�v�ƌ����܂�)�B
�ؖ��@���ɁA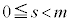 �ƂȂ鐮��s��p���āA
�ƂȂ鐮��s��p���āA
 ����A
����A
 ����B
����B
��2�ʂ�ɏ������Ƃ��܂��B
�A�|�B���A
�܂�A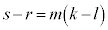 ����C
����C
�ƂȂ�܂����A���̎��́A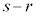 ��
�� �̔{���ł��邱�Ƃ��Ӗ����Ă��܂��B
�̔{���ł��邱�Ƃ��Ӗ����Ă��܂��B
�Ƃ��낪�A �C
�C �Ȃ̂ŁA
�Ȃ̂ŁA �ł��B
�ł��B
 ���傫��m��菬����m�̔{����0��������܂���B�܂�A�C���A
���傫��m��菬����m�̔{����0��������܂���B�܂�A�C���A ����
����
�܂�A ����
���� �ł��B
�ł��B
����́A�A�̌`�ƂȂ鐮��k�Cr ( )������1�ʂ�Ɍ��܂邱�Ƃ��Ӗ����Ă��܂��B(�ؖ��I)
)������1�ʂ�Ɍ��܂邱�Ƃ��Ӗ����Ă��܂��B(�ؖ��I)
2�̐���m�Cn�ɑ��āAm�̔{���ł����āA���An�̔{���ł��鐮����m�Cn�̌��{���ƌ����܂��B
m�Cn�����R���̂Ƃ��ɁA���{���̒��ōŏ��̂��̂��ŏ����{���ƌ����A �Ə����܂��B
�Ə����܂��B
2�̐���m�Cn�ɑ��āAm�̖ł����āA���An�̖ł��鐮����m�Cn�̌��ƌ����܂��B
m�Cn�����R���̂Ƃ��ɁA���̒��ōő�̂��̂��ő�����ƌ����A �Ə����܂��B
�Ə����܂��B
2�̎��R��m�Cn�̍ő����1�̂Ƃ��Am�Cn���݂��ɑf�ł���ƌ����܂��B
1�Ǝ������g�ȊO�̖������Ȃ����R�����f���ƌ����܂��B�f�������������ɕ��ׂ�ƁA2�C3�C5�C7�C11�C13�C17�C19�C23�C29�C31�C37�C41�C43�C47�C������
���R��m���������̑f��p�Cq�C����Cr�̐ς̌` (i�Cj�C����Ck�͎��R��)�ɕ\�����Ƃ��f���������ƌ����܂��B
(i�Cj�C����Ck�͎��R��)�ɕ\�����Ƃ��f���������ƌ����܂��B
a��b�̏������Ȃ����� �ŕ\�����Ƃɂ��܂��B�܂�A
�ŕ\�����Ƃɂ��܂��B�܂�A
�@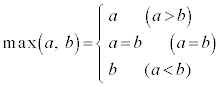
�ł��B���l�ɁAa��b�̑傫���Ȃ����� �ŕ\�����Ƃɂ��܂��B�܂�A
�ŕ\�����Ƃɂ��܂��B�܂�A
�@
�ł��B
2�̎��R��m�Cn�̑f�����������A �C
�C ���Ƃ���ƁA
���Ƃ���ƁA
m�Cn�̍ŏ����{���́A
m�Cn�̍ő���́A
�ł��B
��D54��72�̍ŏ����{���ƍő�����l���܂��B
54�̑f���������́A
72�̑f���������́A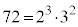
���҂�2���w�����ׂ�ƁA54�ł�1�C72�ł�3�ł��B�傫������3�C����������1�ŁA �C
�C �ł��B
�ł��B
3�̎w�����ׂ�ƁA54�ł�3�C72�ł�2�ł��B �C
�C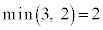
�]���āA54��72�̍ŏ����{���́A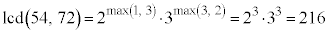
54��72�̍ŏ����{���́A
�Ƃ���ŁA �ł��B�Ȃ��Ȃ�A
�ł��B�Ȃ��Ȃ�A
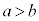 �̂Ƃ��́A
�̂Ƃ��́A �C
�C �ŁA
�ŁA �ł��B
�ł��B
 �̂Ƃ��́A
�̂Ƃ��́A �C
�C �ŁA
�ŁA �ł��B
�ł��B
 �̂Ƃ����A
�̂Ƃ����A �ŁA
�ŁA �ł��B
�ł��B
������A2�̎��R��m�Cn�̑f�����������A �C
�C ���Ƃ��āA
���Ƃ��āA
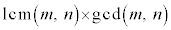



�ƂȂ�A
��C54��72�̍ŏ����{���� �C�ő����
�C�ő����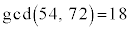
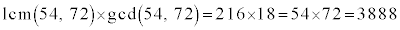 �ł��B
�ł��B
���R��n�̑f����������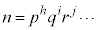 (
( �͎��R��)�Ƃ���ƁAn�̖́A
�͎��R��)�Ƃ���ƁAn�̖́A (
( �͐����ł����āA
�͐����ł����āA �C
�C �C
�C �C���)��
�C���)�� ����܂��B
����܂��B
�̑��a�́A
�Ⴆ�A �̖́A
�̖́A �C
�C �C����C
�C����C ��
�� ����܂��B
����܂��B
504�̖̑��a�́A �ł��B
�ł��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B