実数 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
整数を整数で割るとき、商が整数にならないことがあります。そこで、整数を拡張して有理数という数を考えます。
分母・分子が整数になる分数の形に書ける数を有理数と言います。
整数も分母が1の有理数と見なせば、有理数に含まれます。
有理数同志の和、差、積も有理数です。有理数を0以外の有理数で割ったものも有理数です。
分母が1でない自然数qで、分子が分母と互いに素な整数pであるとき、有理数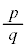
を既約分数と言います。
円周率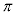
や
，
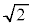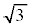は有理数としては表せないことが知られています。
数直線上に目盛りをふることのできる数を実数と言います。
有理数ではない実数を無理数と言います。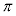
，
，
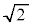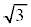は無理数です。
例1．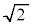
は無理数です。(平方根参照)
なぜなら、仮に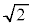
が有理数だとして、既約分数の形に置けたとします。つまり、pを整数，qを自然数だとして、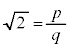
分母を払って2乗すると、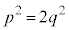
これは、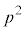
，従って、pが2の倍数だということを意味します。
pが2の倍数のとき、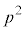
は4の倍数です。
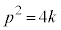とおくと、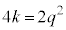
∴ 
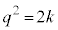
よって、qは2の倍数ですが、p，qが互いに素ではなくなり、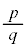
が既約分数であることに反します。
即ち、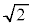
は既約分数の形に表すことができず、有理数ではありません。
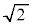は無理数です。
実数同志の和、差、積も実数です。実数を0以外の実数で割ったものも実数です。
実数には、稠密という性質もあって、どのような2個の実数a，bをとっても、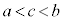
を満たす実数cが存在します。つまり、数直線上に、実数は切れ目なくびっしり並んでいる、ということです。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。