共通テスト数学IA '23年第5問
(1) 円Oに対して、次の手順1で作図を行う。
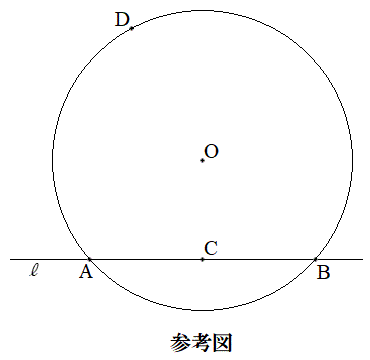 −手順1 −−−−−−−−−−−−
−手順1 −−−−−−−−−−−−(Step 1) 円Oと異なる2点で交わり、中心Oを通らない直線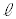 を引く。円Oと直線
を引く。円Oと直線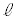 との交点をA,Bとし、線分ABの中点Cをとる。
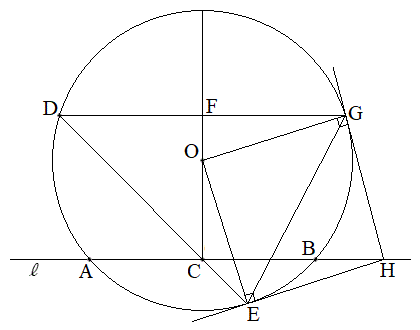
との交点をA,Bとし、線分ABの中点Cをとる。 (Step2) 円Oの周上に、点Dを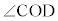 が鈍角となるようにとる。直線CDを引き、円Oとの交点でDとは異なる点をEとする。
が鈍角となるようにとる。直線CDを引き、円Oとの交点でDとは異なる点をEとする。 (Step3) 点Dを通り直線OCに垂直な直線を引き、直線OCとの交点をFとし、円Oとの交点でDとは異なる点をGとする。
(Step4) 点Gにおける円Oの接線を引き、直線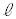 との交点をHとする。
との交点をHとする。 −−−−−−−−−−−−−−−−
このとき、直線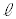 と点Dの位置によらず、直線EHは円Oの接線である。このことは、次の構想に基づいて、後のように説明できる。
と点Dの位置によらず、直線EHは円Oの接線である。このことは、次の構想に基づいて、後のように説明できる。
−構想−−−−−−−−−−−−−
直線EHが円Oの接線であることを証明するためには、
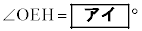 であることを示せばよい。
であることを示せばよい。
−−−−−−−−−−−−−−−−手順1の(Step1)と(Step4)により、4点C,G,H, は同一円周上にあることがわかる。よって、
は同一円周上にあることがわかる。よって、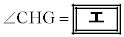 である。一方、点Eは円Oの周上にあることから、
である。一方、点Eは円Oの周上にあることから、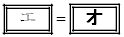 がわかる。よって、
がわかる。よって、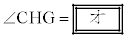 であるので、4点C,H,G,
であるので、4点C,H,G, は同一円周上にある。この円が点
は同一円周上にある。この円が点 を通ることにより、
を通ることにより、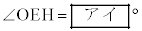 を示すことができる。
を示すことができる。
 の解答群
の解答群  の解答群
の解答群 の解答群
の解答群 の解答群
の解答群
(2) 円Oに対して、(1)の手順1とは直線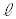 の引き方を変え、次の手順2で作図を行う。
の引き方を変え、次の手順2で作図を行う。
−手順2 −−−−−−−−−−−−
(Step1) 円Oと共有点をもたない直線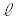 を引く。中心Oから直線
を引く。中心Oから直線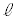 に垂直な直線を引き、直線
に垂直な直線を引き、直線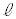 との交点をPとする。
との交点をPとする。 (Step2) 円Oの周上に、点Qを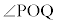 が鈍角となるようにとる。直線PQを引き、円Oとの交点でQとは異なる点をRとする。
が鈍角となるようにとる。直線PQを引き、円Oとの交点でQとは異なる点をRとする。 (Step3) 点Qを通り直線OPに垂直な直線を引き、円Oとの交点でQとは異なる点をSとする。
(Step4) 点Sにおける円Oの接線を引き、直線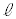 との交点をTとする。
との交点をTとする。 −−−−−−−−−−−−−−−−
このとき、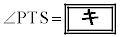 である。
である。
円Oの半径が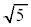 で、
で、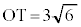 であったとすると、3点O,P,Rを通る円の半径は
であったとすると、3点O,P,Rを通る円の半径は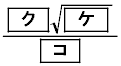 であり、
であり、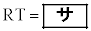 である。
である。
 の解答群
の解答群
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 円に内接する四角形の問題です。手順1と手順2とで円と直線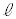 との位置関係が違うのですが、ほぼ同様に考えていけます。というか、手順2でも円と直線
との位置関係が違うのですが、ほぼ同様に考えていけます。というか、手順2でも円と直線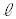 が交わるとして考えると、(1)と(2)は全く同一状況となり、(2)も解答できてしまいます。
が交わるとして考えると、(1)と(2)は全く同一状況となり、(2)も解答できてしまいます。
 (1) 直線EHが円Oの接線であることを示すためには、
(1) 直線EHが円Oの接線であることを示すためには、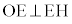 ,つまり、
,つまり、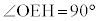 であることを示します。 アイ 90 ......[答]
であることを示します。 アイ 90 ......[答]
円の中心Oと弦ABの中点Cとを結ぶと、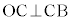 ,つまり、
,つまり、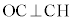
直線GHが円Oの接線であることから、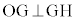
よって、4点C,G,H,Oは同一円周上にあります(円と図形を参照)。 ウ 3 ......[答]四角形COGHは円に内接する四角形で、対向する内角は補角をなすので、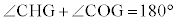 ,一方、
,一方、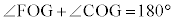 ∴
∴ 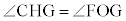 エ 4 ......[答]
エ 4 ......[答]
DとGは直線OCに関する対称点なので、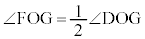 ,一方、
,一方、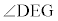 は弦DGの上に立つ円周角で、中心角
は弦DGの上に立つ円周角で、中心角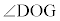 の
の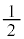 なので、
なので、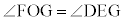 オ 3 ......[答]よって、
オ 3 ......[答]よって、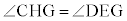 ,つまり、
,つまり、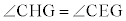
円周角の定理の逆より、4点C,G,H,Eは同一円周上にあります。 カ 2 ......[答]つまり、四角形CHGOの外接円と四角形CGHEの外接円は同一の円で、この外接円は、四角形OGHEの外接円でもあります。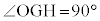 より、これと対向する内角
より、これと対向する内角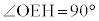 です。また、このことから、線分OHが、この外接円の直径になっていることがわかります。
です。また、このことから、線分OHが、この外接円の直径になっていることがわかります。
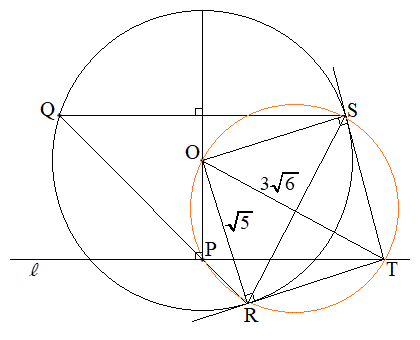
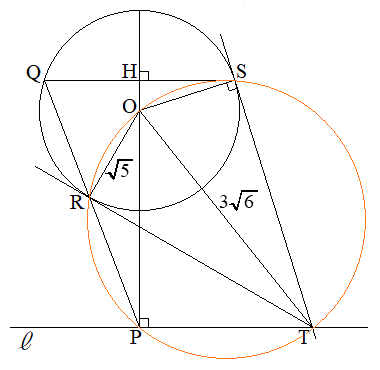 (2) 右図でQから直線OPに下した垂線の足をHとします。
(2) 右図でQから直線OPに下した垂線の足をHとします。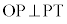 ,
,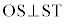 より、四角形OSTPは円に内接する三角形で、
より、四角形OSTPは円に内接する三角形で、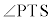 と
と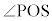 は円に内接する四角形の対角なので互いに補角をなします。よって、
は円に内接する四角形の対角なので互いに補角をなします。よって、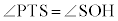 です。
です。QとSは直線OPに関して対称なので、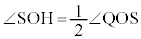 ,また、円周角
,また、円周角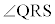 は中心角
は中心角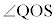 の
の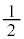 であり、
であり、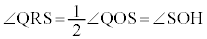
よって、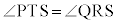 キ 3 ……[答]よって、
キ 3 ……[答]よって、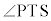 と
と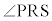 は互いに補角をなし、四角形PRSTは円に内接する四角形であり、5点O,S,T,P,Rは同一円周の点です。また、
は互いに補角をなし、四角形PRSTは円に内接する四角形であり、5点O,S,T,P,Rは同一円周の点です。また、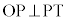 なので、OTはこの円の直径であり、3点O,P,Rを通る円の半径は
なので、OTはこの円の直径であり、3点O,P,Rを通る円の半径は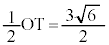 ク 3 ケ 6 コ 2 ......[答]円Oの半径
ク 3 ケ 6 コ 2 ......[答]円Oの半径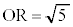 ,
,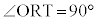 より、
より、 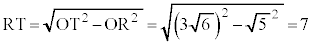 サ 7 ......[答]
サ 7 ......[答]
 注.手順1と手順2で異なる手順に見えますが、手順2でも直線
注.手順1と手順2で異なる手順に見えますが、手順2でも直線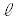 が円と2点で交わるとして考えると、実は、全く同じ状況であって、手順2は、(1)で、C→P,D→Q,E→R,G→S,H→Tとしたものになっています。従って、(1)で
が円と2点で交わるとして考えると、実は、全く同じ状況であって、手順2は、(1)で、C→P,D→Q,E→R,G→S,H→Tとしたものになっています。従って、(1)で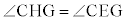 だったことから、
だったことから、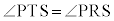 となります。
となります。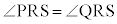 より、
より、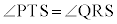 です。
です。また、(1)の結果より、手順2では、四角形OSTRの外接円の直径はOTで、3点O,P,Rを通る円(四角形OSTRの外接円に一致)の半径は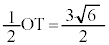 ,円Oの半径
,円Oの半径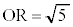 より、
より、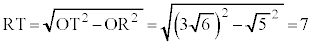 ,として解答できてしまいます。
,として解答できてしまいます。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。  であり、
であり、