共通テスト数学IA '24年第1問
[1] 不等式
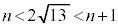 ・・・①
・・・①を満たす整数nは である。実数a,bを
である。実数a,bを 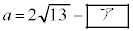 ・・・②
・・・②
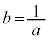 ・・・③
・・・③で定める。このとき
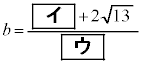 ・・・④
・・・④である。また
である。
①から
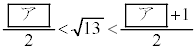 ・・・⑤
・・・⑤が成り立つ。
太郎さんと花子さんは、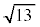 について話している。
について話している。
太郎:⑤から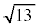 のおよその値がわかるけど、小数点以下はよくわからないね。
のおよその値がわかるけど、小数点以下はよくわからないね。 花子:小数点以下をもう少し詳しく調べることができないかな。
①と④から
を満たす整数mは となる。よって、③から
となる。よって、③から 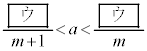 ・・・⑥
・・・⑥が成り立つ。
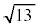 の整数部分は
の整数部分は であり、②と⑥を使えば
であり、②と⑥を使えば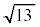 の小数第1位の数字は
の小数第1位の数字は ,小数第2位の数字は
,小数第2位の数字は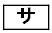 であることがわかる。
であることがわかる。
[2] 以下の問題を解答するにあたっては、必要に応じて問題末の三角比の表を用いてもよい。
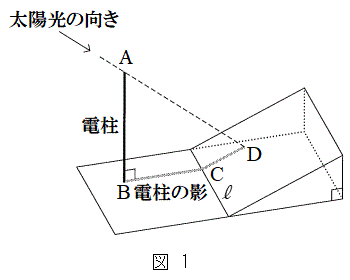 水平な地面(以下、地面)に垂直に立っている電柱の高さを、その影の長さと太陽高度を利用して求めよう。
水平な地面(以下、地面)に垂直に立っている電柱の高さを、その影の長さと太陽高度を利用して求めよう。
図1のように、電柱の影の先端は坂の斜面(以下、坂)にあるとする。また、坂には傾斜を表す道路標識が設置されていて、そこには7%と表示されているとする。
電柱の太さと影の幅は無視して考えるものとする。また、地面と坂は平面であるとし、地面と坂が交わってできる直線を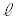 とする。
とする。
電柱の先端を点Aとし、根もとを点Bとする。電柱の影について、地面にある部分を線分BCとし、坂にある部分を線分CDとする。線分BC,CDがそれぞれ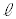 と垂直であるとき、電柱の影は坂に向ってまっすぐにのびているということにする。
と垂直であるとき、電柱の影は坂に向ってまっすぐにのびているということにする。
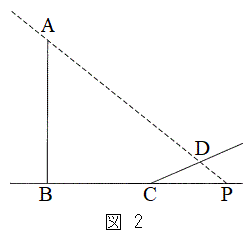 電柱の影が坂に向ってまっすぐにのびているとする。このとき、4点A,B,C,Dを通る平面は
電柱の影が坂に向ってまっすぐにのびているとする。このとき、4点A,B,C,Dを通る平面は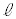 と垂直である。その平面において、図2のように、直線ADと直線BCの交点をPとすると、太陽高度とは
と垂直である。その平面において、図2のように、直線ADと直線BCの交点をPとすると、太陽高度とは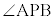 の大きさのことである。
の大きさのことである。
道路標識の7%という表示は、この坂をのぼったとき、100mの水平距離に対いて7mの割合で高くなることを示している。nを1以上9以下の整数とするとき、坂の傾斜角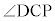 の大きさについて
の大きさについてを満たすnの値は である。
である。
以下では、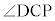 の大きさは、ちょうど
の大きさは、ちょうど であるとする。
であるとする。
ある日、電柱の影が坂に向ってまっすぐにのびていたとき、影の長さを調べたところ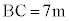 ,
,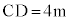 であり、太陽高度は
であり、太陽高度は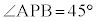 であった。点Dから直線ABに垂直な直線を引き、直線ABとの交点をEとするとき
であった。点Dから直線ABに垂直な直線を引き、直線ABとの交点をEとするとき であり
である。よって、電柱の高さは、小数第2位で四捨五入すると であることがわかる。
であることがわかる。
 ,
,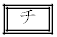 の解答群(同じものを繰り返し選んでもよい。)
の解答群(同じものを繰り返し選んでもよい。)
 の解答群
の解答群 10.4
10.4  10.7
10.7  11.0
11.0 11.3
11.3  11.6
11.6  11.9
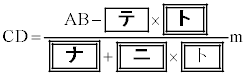
11.9別の日、電柱の影が坂に向ってまっすぐにのびていたときの太陽高度は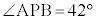 であった。電柱の高さがわかったので、前回調べた日からの影の長さの変化を知ることができる。電柱の影について、坂にある部分の長さは
であった。電柱の高さがわかったので、前回調べた日からの影の長さの変化を知ることができる。電柱の影について、坂にある部分の長さは である。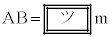 として、これを計算することにより、この日の電柱の影について、坂にある部分の長さは、前回調べた4mより約1.2mだけ長いことがわかる。
として、これを計算することにより、この日の電柱の影について、坂にある部分の長さは、前回調べた4mより約1.2mだけ長いことがわかる。
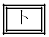 ,
, の解答群(同じものを繰り返し選んでもよい。)
の解答群(同じものを繰り返し選んでもよい。)
三角比の表
| 角 | 正弦(sin) | 余弦(cos) | 正接(tan) | | 角 | 正弦(sin) | 余弦(cos) | 正接(tan) |
| 0° | 0.0000 | 1.0000 | 0.0000 | | 45° | 0.7071 | 0.7071 | 1.0000 |
| 1° | 0.0175 | 0.9998 | 0.0175 | | 46° | 0.7193 | 0.6947 | 1.0355 |
| 2° | 0.0349 | 0.9994 | 0.0349 | | 47° | 0.7314 | 0.6820 | 1.0724 |
| 3° | 0.0523 | 0.9986 | 0.0524 | | 48° | 0.7431 | 0.6691 | 1.1106 |
| 4° | 0.0698 | 0.9976 | 0.0699 | | 49° | 0.7547 | 0.6561 | 1.1504 |
| 5° | 0.0872 | 0.9962 | 0.0875 | | 50° | 0.7660 | 0.6428 | 1.1918 |
| 6° | 0.1045 | 0.9945 | 0.1051 | | 51° | 0.7771 | 0.6293 | 1.2349 |
| 7° | 0.1219 | 0.9925 | 0.1228 | | 52° | 0.7880 | 0.6157 | 1.2799 |
| 8° | 0.1392 | 0.9903 | 0.1405 | | 53° | 0.7986 | 0.6018 | 1.3270 |
| 9° | 0.1564 | 0.9877 | 0.1584 | | 54° | 0.8090 | 0.5878 | 1.3764 |
| 10° | 0.1736 | 0.9848 | 0.1763 | | 55° | 0.8192 | 0.5736 | 1.4281 |
| 11° | 0.1908 | 0.9816 | 0.1944 | | 56° | 0.8290 | 0.5592 | 1.4826 |
| 12° | 0.2079 | 0.9781 | 0.2126 | | 57° | 0.8387 | 0.5446 | 1.5399 |
| 13° | 0.2250 | 0.9744 | 0.2309 | | 58° | 0.8480 | 0.5299 | 1.6003 |
| 14° | 0.2419 | 0.9703 | 0.2493 | | 59° | 0.8572 | 0.5150 | 1.6643 |
| 15° | 0.2588 | 0.9659 | 0.2679 | | 60° | 0.8660 | 0.5000 | 1.7321 |
| 16° | 0.2756 | 0.9613 | 0.2867 | | 61° | 0.8746 | 0.4848 | 1.8040 |
| 17° | 0.2924 | 0.9563 | 0.3057 | | 62° | 0.8829 | 0.4695 | 1.8807 |
| 18° | 0.3090 | 0.9511 | 0.3249 | | 63° | 0.8910 | 0.4540 | 1.9626 |
| 19° | 0.3256 | 0.9455 | 0.3443 | | 64° | 0.8988 | 0.4384 | 2.0503 |
| 20° | 0.3420 | 0.9397 | 0.3640 | | 65° | 0.9063 | 0.4226 | 2.1445 |
| 21° | 0.3584 | 0.9336 | 0.3839 | | 66° | 0.9135 | 0.4067 | 2.2460 |
| 22° | 0.3746 | 0.9272 | 0.4040 | | 67° | 0.9205 | 0.3907 | 2.3559 |
| 23° | 0.3907 | 0.9205 | 0.4245 | | 68° | 0.9272 | 0.3746 | 2.4751 |
| 24° | 0.4067 | 0.9135 | 0.4452 | | 69° | 0.9336 | 0.3584 | 2.6051 |
| 25° | 0.4226 | 0.9063 | 0.4663 | | 70° | 0.9397 | 0.3420 | 2.7475 |
| 26° | 0.4384 | 0.8988 | 0.4877 | | 71° | 0.9455 | 0.3256 | 2.9042 |
| 27° | 0.4540 | 0.8910 | 0.5095 | | 72° | 0.9511 | 0.3090 | 3.0777 |
| 28° | 0.4695 | 0.8829 | 0.5317 | | 73° | 0.9563 | 0.2924 | 3.2709 |
| 29° | 0.4848 | 0.8746 | 0.5543 | | 74° | 0.9613 | 0.2756 | 3.4874 |
| 30° | 0.5000 | 0.8660 | 0.5774 | | 75° | 0.9659 | 0.2588 | 3.7321 |
| 31° | 0.5150 | 0.8572 | 0.6009 | | 76° | 0.9703 | 0.2419 | 4.0108 |
| 32° | 0.5299 | 0.8480 | 0.6249 | | 77° | 0.9744 | 0.2250 | 4.3315 |
| 33° | 0.5446 | 0.8387 | 0.6494 | | 78° | 0.9781 | 0.2079 | 4.7046 |
| 34° | 0.5592 | 0.8290 | 0.6745 | | 79° | 0.9816 | 0.1908 | 5.1446 |
| 35° | 0.5736 | 0.8192 | 0.7002 | | 80° | 0.9848 | 0.1736 | 5.6713 |
| 36° | 0.5878 | 0.8090 | 0.7265 | | 81° | 0.9877 | 0.1564 | 6.3138 |
| 37° | 0.6018 | 0.7986 | 0.7536 | | 82° | 0.9903 | 0.1392 | 7.1154 |
| 38° | 0.6157 | 0.7880 | 0.7813 | | 83° | 0.9925 | 0.1219 | 8.1443 |
| 39° | 0.6293 | 0.7771 | 0.8098 | | 84° | 0.9945 | 0.1045 | 9.5144 |
| 40° | 0.6428 | 0.7660 | 0.8391 | | 85° | 0.9962 | 0.0872 | 11.4301 |
| 41° | 0.6561 | 0.7547 | 0.8693 | | 86° | 0.9976 | 0.0698 | 14.3007 |
| 42° | 0.6691 | 0.7431 | 0.9004 | | 87° | 0.9986 | 0.0523 | 19.0811 |
| 43° | 0.6820 | 0.7314 | 0.9325 | | 88° | 0.9994 | 0.0349 | 28.6363 |
| 44° | 0.6947 | 0.7193 | 0.9657 | | 89° | 0.9998 | 0.0175 | 57.2900 |
| 45° | 0.7071 | 0.7071 | 1.0000 | | 90° | 1.0000 | 0.0000 | - |
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 昨年の第1問より難易度がぐんと上がっていて、基礎学力を見る共通テストとしては、由々しきことだと思います。
[1] ①両辺を2乗すると、
両者を比較して、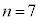 ア 7 .......[答]よって、②は、
ア 7 .......[答]よって、②は、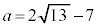
③より、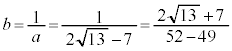 (分母の有理化を参照)
(分母の有理化を参照) 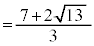 イ 7 ウ 3 ......[答]
イ 7 ウ 3 ......[答]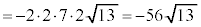 エオカ
エオカ 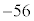 ......[答]
......[答]①より、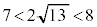
これと④より、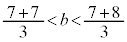 ,即ち、
,即ち、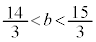
よって、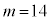 キク 14 ......[答]
キク 14 ......[答]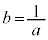 より、
より、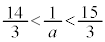
よって⑥は、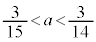 (不等式を参照)
(不等式を参照)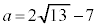 より、
より、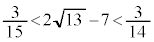
∴ 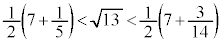
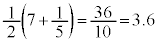 ,
,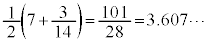 より、
より、 これより、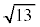 の整数部分は3,小数第1位の数字は6,小数第2位の数字は0です。 ケ 3 コ 6 サ 0 ......[答]
の整数部分は3,小数第1位の数字は6,小数第2位の数字は0です。 ケ 3 コ 6 サ 0 ......[答]
(2) 三角比の表を見ると、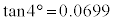 ,
,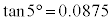 なので、
なので、 よって、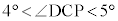
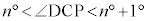 を満たすnの値は4 シ 4 ......[答]
を満たすnの値は4 シ 4 ......[答]
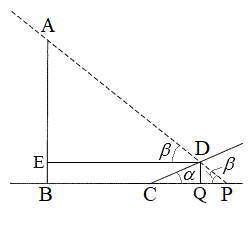 Dから直線BPに垂線を下し、垂線の足をQとします。また、Dから直線ABに下した垂線の足がEです。
Dから直線BPに垂線を下し、垂線の足をQとします。また、Dから直線ABに下した垂線の足がEです。
以下、斜面の傾角を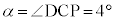 とします。右図より、
とします。右図より、 ス 4 セ 0 ......[答]
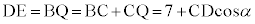 ・・・⑦
・・・⑦ソ 7 タ 4 チ2 ......[答]太陽高度を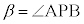 とします。ここでは、
とします。ここでは、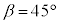 です。また、
です。また、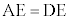 です。
です。
三角比の表より、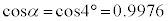 ,
,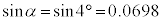
電柱の高さは、⑦より、 ツ 3 ......[答]別の日の場合は、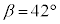 です。⑦より、
です。⑦より、 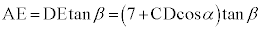 ・・・⑧
・・・⑧また、
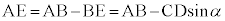 ・・・⑨
・・・⑨⑧,⑨より、
∴ 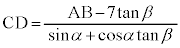 テ 7 ト 5 ナ 0 ニ 1 ......[答]
テ 7 ト 5 ナ 0 ニ 1 ......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。  ・・・④
・・・④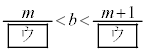
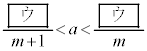 ・・・⑥
・・・⑥